Построение графиков нескольких неявных функций
Построение таких графиков теоретически сводится к построению графика одной неявной функции. Пусть нужно построить графики неявных функций, заданных уравнениями:
F1(х, у) = Ф1(х, у), F2 (х, у) = Ф2(х, у), F3 (х, у) = Ф3(х, у),…, Fn (x, у) = Фn(х, у).
Тогда мы можем привести эти уравнения к виду:
F1(х, у) – Ф1(х, у) = 0, F2 (х, у) -Ф2(х, у) = 0, F3 (х, у) -Ф3(х, у) = 0,…, Fn (х, у) -Фn(х, у) = 0 и построить график:
(F1 (х, у) -Ф1(х, у))(F2(х, у) -Ф2(х, у))(F3 (х, у) -Ф3(х, у))…(Fn (х, у) -Фn(х, у)) = 0.
Но на практике лучше поступать не так, а совсем наоборот. Например, построение графика:
ImplicitPlotf ((42-38*Sign[x])y+x^(x-2) ^2/100) ^ (1/3) - 1) (Sqrt [13-4x]+1)) (9*Sqrt[5]-x(x-1)Sqrt[x+2])(4x^2+16y^2+56x-64y+259)==0, {x,-2.13/4), PlotPoints > 25]; //TimingМожно заменить построением следующего графика.
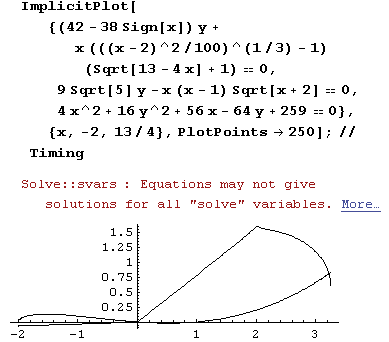
График:
ImplicitPlot[((4y+x ^ 2) ^ 2+Sign[x ^ 2+2x]+1) ((x ^ 2+y ^ 2) ^ (5/2)-4x(x ^ 2-y ^ 2))==0, {x,-5.5}, PlotPoints > 25]; //TimingМожно строить часами, а график:

Строится всего за 21.641 секунды.
