Аналитическая геометрия на плоскости, или 2D-графика. Графические примитивы.
Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу – и обозначить их числами.
В XIV в. французский математик Н. Оресм ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.
Это нововведение оказалось чрезвычайно продуктивным…
Графические примитивы в графике играют ту же роль, что и основные фигуры в геометрии. Именно из них составляются все остальные фигуры.
Многоугольник – примитив Polygon
Графический примитив Polygon[ {{х1, y1 ], (х2, у2},…}] представляет собой закрашенный многоугольник, ограниченный замкнутой ломаной линий, проходящей через точки {х1, y1 }, {х2, у2),…. Вот как рисуется равносторонний треугольник салатного цвета.
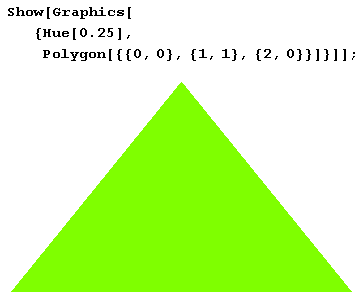
Прямоугольник – примитив Rectangle
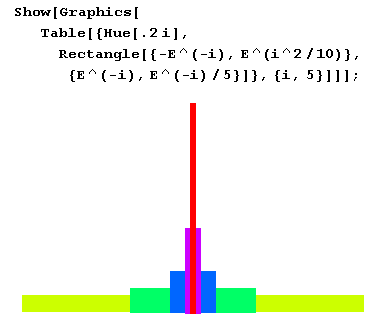
Частный случай многоугольника – прямоугольник – можно получить с помощью примитива Rectangle [{xmin, ymin}, {х mах, у mах} ], в котором (xmin, ymin) – координаты левого нижнего угла прямоугольника, а {х mах, у mах} – координаты правого верхнего угла прямоугольника. Показанная ниже фигура состоит из пяти прямоугольников. Все они имеют разный цвет.