Аналитическая геометрия на плоскости, или 2D-графика. Графические примитивы.
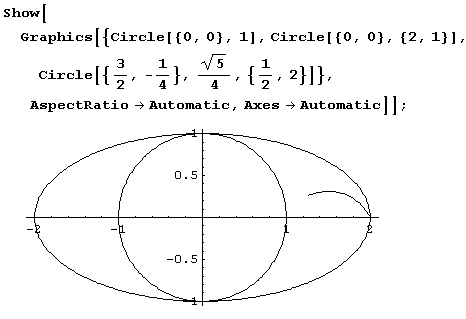
Эллипс и его дуга – примитив Circle
Дугу эллипса с полуосями r х и r у создает графический примитив circle [ {х, у], (r х, r у}] – Здесь {х, у] – координаты центра эллипса. Графический примитив Circle[{х, у], { r х, r у}, {th1, th2}] рисует дугу эллипса, которая получается из соответствующей дуги окружности. Центр эллипса находится в точке с координатами [х, у], r х и r у – полуоси, a (th1, th2] – граничные значения полярного угла для дуги окружности. Чтобы нарисовать эллипс, достаточно вызвать примитив circle ({x, у], (r х, r у}].
Ниже нарисован эллипс, окружность, диаметр которой совпадает с меньшей осью эллипса, и дуга окружности.
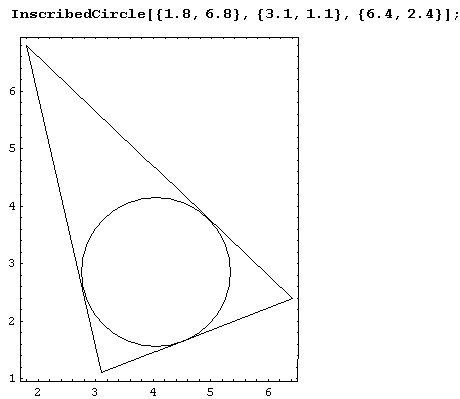
Пример 9.2. Окружность, вписанная в треугольник.
Давайте напишем функцию inscribedcircle, которая по заданному своими вершинами треугольнику вписывает в него окружность. Предварительно нам понадобится функция, назовем ее inscribedCircleData, которая вычисляет радиус и координаты центра окружности, вписанной в треугольник.
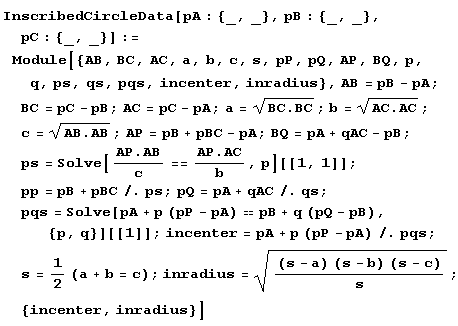
Теперь можем написать функцию, отображающую стороны треугольника и вписанную в него окружность.

(Здесь Sequence превращает Sequence@@InscribedCircleData[pA,pB,pC] в Sequence [рА,рВ,рС].)
Теперь можем приступить к рисованию.