Построение графиков функций, заданных параметрически (функция ParametricPlot)
Функция ParametricPlot позволяет рисовать кривые и семейства кривых, заданных параметрически. Эта функция имеет те же опции, что и функция Plot. В некотором смысле эта функция универсальна. Если не учитывать неявно заданных функций, то именно функция ParametricPlot позволяет построить графики всех мыслимых функций, включая и многозначные.
Без проблем строятся и графики, заданные в полярной системе координат. Фигуры Лиссажу, кривые Уатта, овалы Кассини, Декарта, Мюнгера, улитки Паскаля, однолистники, листы Декарта, всевозможные розы и розетки, рулеты, годографы, эволюты и эвольвенты всех мыслимых и немыслимых кривых, циклоиды, всевозможные спирали, циссоиды, конхоиды, строфоиды, астроиды, кардиоиды, неоиды, лемнискаты, узлы, квадратрисы, клотоиды, кохлеоиды, трохоиды, элипсиды, катакаустики, всевозможные параболы, локсодромы и лоциклики, трезубцы, трисектрисы, трилистники, верзиеры, брахистохроны, подэры, кривые с именами древнегреческих и средневековых ученых – вот далеко не полный перечень всевозможного зверья, которое может быть нарисовано функцией ParametricPlot.
Пример 9.3. Фигуры Лиссажу.
Это классический пример применения функции ParametricPlot. Рисуются эти фигуры совсем просто, и потому мы нарисуем сразу несколько.

Пример 9.4. Розы и розетки.
Эти цветы весьма многочисленны, выглядят, как правило, очень мило и легко рисуются. Процесс вычерчивания совсем прост, если предварительно определить следующую функцию.
PolarR[a1,a2_,omega_,phi_] := Module[{r=a1+a2*Cos[omega*phi]},<r*Coi[phi],r*Sin[phi]}]Вот как, например, с помощью этой функции рисуется многолепестковая роза.
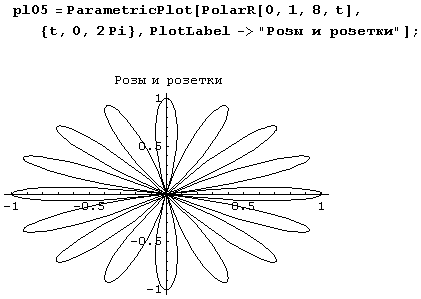
А вот еще один милый цветок.
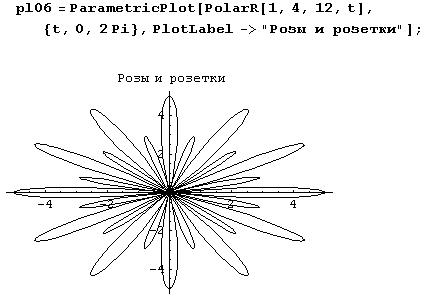
Цветы эти столь разнообразны, что согласия относительно количества их видов нет. Одни насчитывают более полтора десятка видов, другие – не менее сотни.
