Построение графиков функций, заданных параметрически (функция ParametricPlot)
Пример 9.7. Годографы.
Иногда приходится вычерчивать годографы семейства вектор-функций, заданных в полярных координатах. В определении такой функции часто участвует некий вектор (очень часто единичный), который с течением времени вращается вокруг начала координат. Пусть, например, нужно вычертить годограф вектор-функции r(t) = аte + Rt+a (e) + АRwt+p (e), где e – единичный вектор, Rф – поворот на угол ф вокруг начала координат, а а, а, А, w, p – заданные параметры. Тогда, чтобы упростить определение функции PolarXYAB, можно поступить так. Сначала определим следующую функцию.
Rphi[phi_] := {Cos[phi],Sin[phi]}С ее помощью значительно упрощается определение функции PolarXYAB, которое упрощает задание кривой семейства.
PolarXYAB[t_,a_,alpha_,aa_,omega_,beta_] := {0,a*t}+Rphi[t+alpha]+aa*Rphi[omega*t+beta]Вот как, например, с помощью этой функции рисуется одна из кривых семейства.
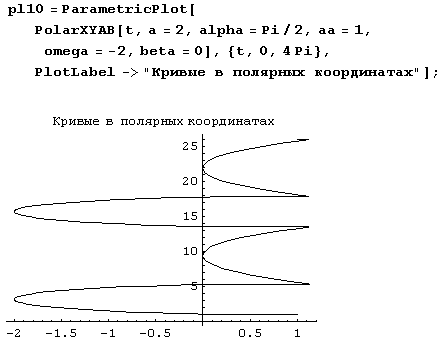
Как вам эта зверушка? Если думаете, что они все такие, вы ошибаетесь.
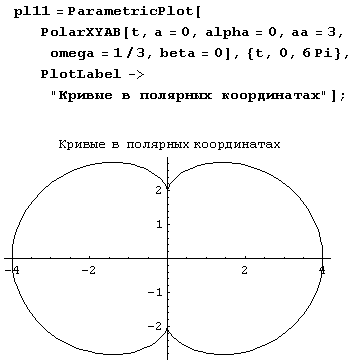
Вращающийся единичный вектор очень часто полезен и при вычерчивании других кривых, например циклоид.
