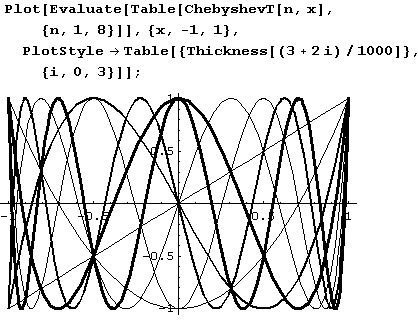
Вычерчивание графиков. Функция Plot.
Пусть функции, графики которых мы хотим построить, получаются с помощью функции Table или NDSolve. Для определенности пусть это будут полиномы Чебышева. Следующая строка ошибочна.
Plot[Table[ChebyshevT[n,x],{n,1,4}],{x,-1.1})Дело в том, что здесь система Mathematica не сможет вычислить функции. Почему? Давайте разберемся. Начнем сначала.
Вот график, который строится без проблем.
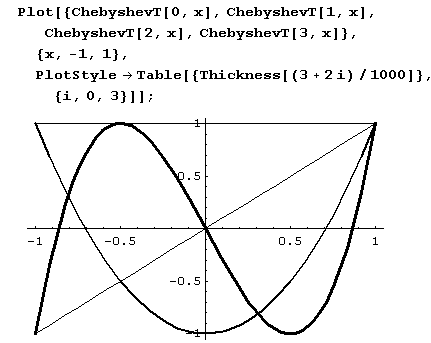
Здесь построены графики первых четырех полиномов Чебышева первого рода: ChebyshevT[ 0, x] – полином нулевого порядка, равный тождественно единице, ChebyshevT[l,x] = х, а также полиномы ChebyshevT[2,z] и ChebyshevT[ 3,x].
Но вот так график построить не удастся.
list01={ChebyshevT[0,x],ChebyshevT[1,x],ChebyshevT[2,x],ChebyshevT[3,x]} {1, x, -1 + 2x2, -3x + 4x3} Plottlist 0 1,{x,-1.1}]; Plot::plnr: list 0 1 is not a machine-size real number at x =-1.. More...Оказывается, система Mathematica не может вычислить значения list01! Почему? Потому что функция Plot имеет атрибут HoldAll.
Attributes[Plot] {HoldAll,Protected)Этот атрибут указывает, что аргументы функций вычисляться не должны. Обычно аргументы функций вычисляются.
hh[1+2.2+3.3+4] hh[3.5.7]Но если функции приписать атрибут HoldAll, вычисления аргументов выполняться не будут.
SetAttributes[hh,HoldAll] hh[1+2.2+3.3+4] hh[1+2.2+3.3+4]Чтобы в таких случаях выполнить вычисления, можно использовать функцию Evaluate. Выражение Plot [Evaluate [list0l], {x,-1, 1} ]; строит предыдущий график без проблем.
Ниже построены графики 8 полиномов Чебышева.