Специальные типы графиков
Как мы видели, функция ParametricPlot практически универсальна. Однако часто приходится строить графики специального вида. Тогда можно воспользоваться более специализированными функциями.
Графики в полярной системе координат
Построение графиков в полярной системе координат зачастую упрощается, если воспользоваться функцией PolarPlot из пакета Graphics`Graphics`. Пакет этот загружается как обычно. <<Graphics` Graphics`.
Ниже показано, как нарисовать эллипс и улитку на одном графике.
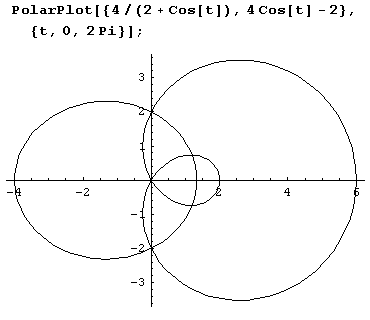
Пример 9.13. Несколько графиков в разных системах координат на одном чертеже.
Иногда на одном листе (чертеже) нужно начертить несколько графиков, притом в разных системах координат. Предположим, на одном листе нужно начертить четыре графика, расположив их в два ряда по два графика, т.е. два графика в верхнем ряду и два – в нижнем. Два графика создадим с помощью функции ParametricPlot, а два – с помощью функции PolarPlot. Сначала загружаем нужный графический пакет.
<<Graphics `Graphics`А теперь задаем радиус-вектор как функцию угла:
Clearr[r] r[theta_]=Sin[8 theta/7];И определяем первый график.
ppl=ParametricPlot[{r[theta]Cos[theta],r[theta]Sin[theta]}, {theta,0.14Pi},AspectRatio > Automatic,DisplayFunction > Identity];После этого точно так же готовим второй график.
Clear[r] r[theta_]=theta*Cos[ theta]; pp2=ParametricPlot[{r[theta]Cos[theta],r[theta]Sin[theta]}, {theta,-19Pi/2.19Pi/2},AspectRatio > Automatic,PlotPoints > 200, DisplayFunction > Identity];Аналогично строим третий график, но в полярных координатах с помощью функции PolarPlot.
Clear[r] r[theta_]=Exp[Cos[ theta]]-2Cos[4theta]+Sin[theta/12]^5; pp3=PolarPlot[r[theta],{theta,0.24Pi},AspectRatio > Automatic, PlotPoints > 200,PlotRange > {{-4.5},{-4.5.4.5}}, DisplayFunction > Identity];Последний, четвертый, график тоже строим в полярных координатах с помощью функции PolarPlot.
Cleart[r] pp4=PolarPlot[{Sqrt[1/theta],-Sqrt[I/theta]},{theta,0.1,10Pi}, AspectRatio > Automatic,PlotPoints > 200, PlotRange > All,DisplayFunction > Identity];