Построение графиков неявно заданных функций (функция ImplicitPlot пакета Graphics`ImplicitPlot`)
Пример 9.17. Кривая x5 + у5 = ху2.
Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-1, 1).
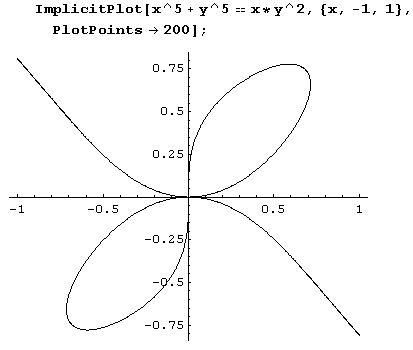
График опять вычерчен очень аккуратно и весьма точно. И опять очень трудно отличить криволинейную дугу от отрезка прямой, и из-за этого абсциссы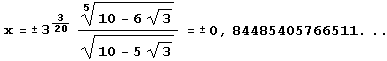 
точек перегиба в II и IV квадрантах определить на глаз почти невозможно.
Исследованием также находятся абсциссы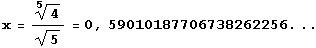 
точек локальных экстремумов в I и III квадрантах, а также уравнения вертикальных касательных 
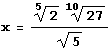(х=±0.714261716914966914109…). Наличие асимптоты х+у = 0 определяется по уравнению x+ y = ху2 с первого взгляда.
Трудные случаи построения графика неявно заданной функции одной переменной в заданном интервале изменения переменной с помощью функции ImplicitPlot
Построение графика неявно заданной функции одной переменной даже в заданном интервале изменения переменной – весьма непростая задача. Функция ImplicitPlot во многих случаях справляется с ней блестяще. Но далеко не во всех случаях. Вот тривиальный пример.
ImplicitPlot[Min[x,y]==1,(x,-22.22},PlotPoints > 200]; Solve::dinv: The expression Min'0'1* [x, y] involves unknowns in more than one argument, so inverse functions cannot be used. More... ImplicitPlot::epfail: Equation Min[x,y]==1could not be solved for points to plot.Конечно, уравнение Min[x,y]= =1 определяет неявно заданную функцию, график которой представляет собой прямой угол с вершиной в точке (1; 1), причем стороны его параллельны осям координат. Потому с этим примером должен без труда справляться даже шестиклассник. Впрочем, функция ImplicitPlot с этим графиком тоже может справиться, но после некоторой подсказки.
Вот еще один трудный (для функции ImplicitPlot) случай.
С этим примером должен без труда справляться даже восьмиклассник. (Правда, если он хочет участвовать в районной (городской) олимпиаде или поступить на мехмат.)