Построение графиков неявно заданных функций (функция ImplicitPlot пакета Graphics`ImplicitPlot`)
Построение графика неявно заданной функции одной переменной при изменении переменной на заданном интервале, из которого исключено несколько точек
Чтобы построить график решения уравнения, найденного функцией Solve на интервале изменения переменной (xmin, xmax), из которого исключено несколько точек, нужно в вызове функции ImplicitPlot [уравнение, (переменная, xmin, xmax}] между xmin, и хmах через запятую перечислить все исключаемые точки. Впрочем, функция ImplicitPlot, как правило, сама избегает значений, которые доставляют хлопоты, и потому прибегать к этой форме вызова не приходится даже в следующих двух классических случаях.
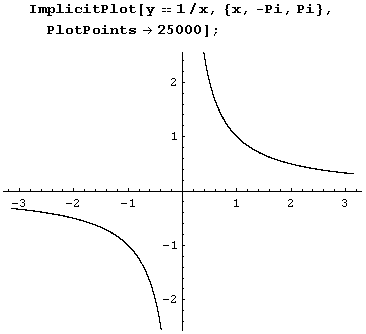
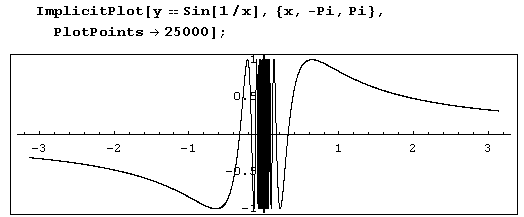
Построение графика неявно заданной функции одной переменной при изменении переменных на заданных интервалах методом нахождения линии уровня
Уравнение F, (х, у) = F2 (х, у) можно записать в виде F, (х, у) -F, (х, у) = 0. Так что фактически вместо решения уравнения F, (х, у) = F2 (х, у) можно найти линию уровня функции F, (х, у) -F2 (х, у), на которой она равна 0. Как дать такую подсказку функции ImplicitPlot? Очень просто: нужно указать интервалы изменения обеих переменных.
Рассмотрим примеры, когда это полезно.
Ранее с помощью вызова ImplicitPlot[Min[x,у] ==1, {x,-22.22},PlotPoints › 200]; мы не смогли построить график неявной функции Min[x,y]==l. А вот с подсказкой ImplicitPlot[Min[x,y]==l,{х,-22.22},(у,-22.22},PlotPoints › 200]; график строится мгновенно. Вызов:
ImplicitPlot[ (x^2+y^2-25) (16 x^2+y^2-4)**(x^2+16y^2-96y+140) (4x^2-16x*Sign[x]+4y^2-16y+31)==0, {x,-5.5}, (y,-5.5), PlotPoints > 25];Строит график более десяти минут, а вызов:
ImplicitPlot [(x^2+y-2-25) (16 x^2+y^2-4) (x^2+16y^2-96y+140) (4x^2-16x*Sign[x]+4y^2-16y+31)==0, {x,-5.5}, {y,-5.5), plotPoints > 250];Нужно менее трети секунды.
