Построение графиков неявно заданных функций (функция ImplicitPlot пакета Graphics`ImplicitPlot`)
Пример 9.15. Кривая х4 + у4 = х2 + у2.
Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что в полярных координатах она задается уравнением вида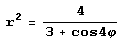 
и потому вся лежит внутри окружности радиуса 
.
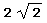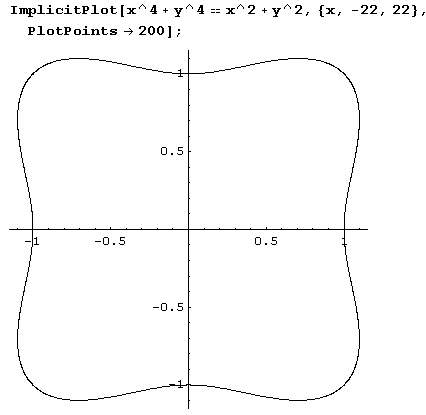
Заметьте, что хотя для х интервал изменения был взят с большим запасом, график увеличен за счет того, что функция ImplicitPlot сообразила, что отображать весь заданный интервал нет необходимости.
Пример 9.16. Кривая у5 + x4 = ху2.
Эта кривая с помощью функции ImplicitPlot рисуется совсем просто, если заметить, что все интересные детали лежат в интервале (-10, 10).
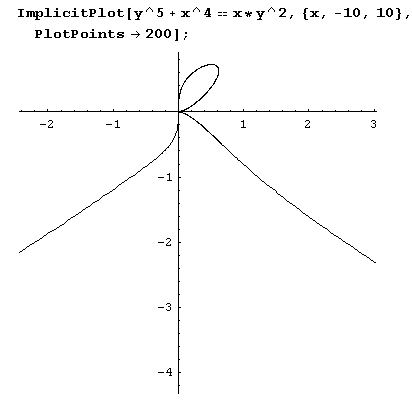
По поводу этого и других графиков неявно заданных функций нужно сделать следующее замечание. Система Mathematica вычерчивает графики очень аккуратно и весьма точно. Однако в случае неявно заданных функций свойства вычерчиваемых кривых далеко не всегда очевидны из уравнения. Аккуратное вычерчивание иногда также может скрывать эти свойства. Например, иногда очень трудно отличить криволинейную дугу от отрезка прямой, а из-за этого можно пропустить точку перегиба. В ГУ квадранте вычерченного системой Mathematica графика, например, есть точка перегиба. Однако на глаз заметить ее очень трудно, поскольку криволинейная дуга почти сливается с прямой.
В учебных пособиях в таких случаях обычно жертвуют точностью и приводят эскиз графика, на котором характерные точки кривой легко заметны на глаз. Система Mathematica же точностью жертвовать не может, и потому иногда требуется дополнительное исследование графика, которое можно провести, конечно же, с помощью системы Mathematica.
В первом квадранте, например,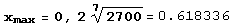 
а максимум функция у(х) достигает при 
.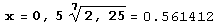