Построение графиков нескольких неявных функций
Так же легко вычерчивается и следующий график.
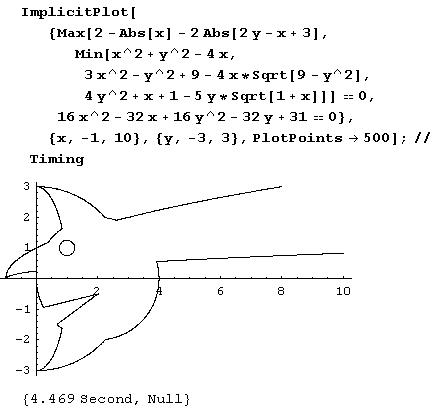
График же:
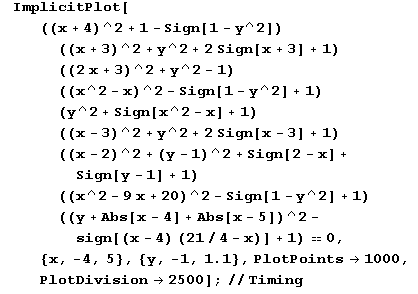
Построению почти не поддается: при изменении параметров PlotPoints › l000, PlotDivision › 2500 в нем часто исчезают те или иные детали. Не удается его построить ни вот так:
ImplicitPlott((x+4)^2+1-Sigm[1-y^2]) ((x+3)^2+y^2+2*Sign[x+3]+1) ((2x+3)^2+y^2-1)((x^2-x)^2-Sign[1-y^2]+1) (y^2+Sign[x^2-x]+1) ((x-3)^2+y^2+2*Sign[x-3]+1) ((x-2)^2+(y-1)^2+Sign[2-x]+Sign[y-1]+1) ((x^2-9x+20)^2-Sign[1-y^2]+1) ((y+Abs[x-4]+Abs[x-5])^2-Sign[(x-4)(21/4-x)]+1)==0, (x,-4.5}, PlotPoints > 1000,PlotDivision > 250];Ни вот так:
ImplicitPlott{(x+4)^2+1-Sign[1-y^2]==0, (x+3)^2+y^2+2*Sign[x+3]+1==0, (2x+3)^2+y^2-1==0, (x^2-x)^2-Sign[1-y^2]+1==0, y^2+Sign[x^2-x]+1==0, (x-3)^2+y^2+2*Sign[x-3]+1==0, (x-2)^2+(y-1)^2+Sign[2-x]+Sign[y-1]+l==0, (x^2-9x+20)^2-Sign[1-y^2]+l==0, (y+Abs[x-4]+Abs[x-5])^2-Sign[(x-4)(21/4-x)]+1==0}, {x,-4.5},PlotPoints > 1000, PlotDivision > 250];В лучшем случае получаем кучу предупреждений и вот что:
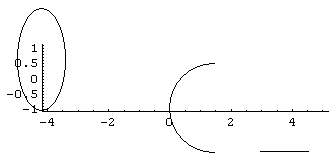
Мораль: графики многих неявных функций легко строятся с помощью функции ImplicitPlot, однако существуют невинно выглядящие мехматовские "приколы", при построении которых либо теряются дуги, отдельные точки, отрезки, либо же графики не строятся совсем. Иногда проблем удается избежать, если изменить метод построения графика (от решения уравнения перейти к построению линии уровня или наоборот). Однако это помогает далеко не всегда. Тогда приходится брать мехматовские учебники. Они не покажутся такими недоступными, если вы будете читать их, а система Mathematica будет делать то, что там написано! Очень часто всего лишь нескольких подстановок (их может выполнить система Mathematica) достаточно, чтобы перейти к параметрическому заданию графика.
