Аппроксимации рядом Тейлора
Начнем с аппроксимации функции хорошо известным рядом Тейлора степени 8 относительно середины интервала (точки с х=2):
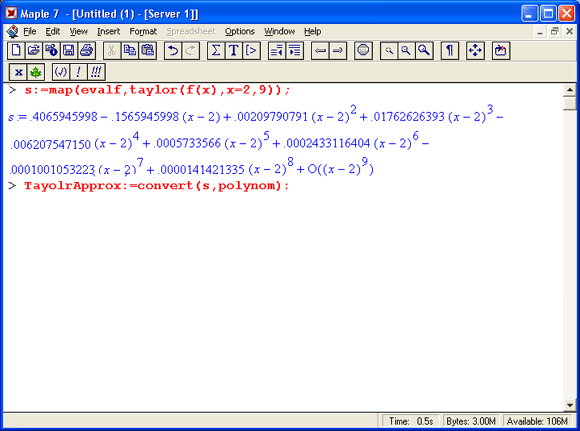
Такой ряд позволяет использовать для вычислений только арифметические действия, что само по себе здорово! Для удобства преобразуем аппроксимацию в функцию, чтобы она соответствовала форме, указанной для первоначальной функции f(x). Тогда мы сможем построить график кривой ошибок для аппроксимации полиномом Тейлора:
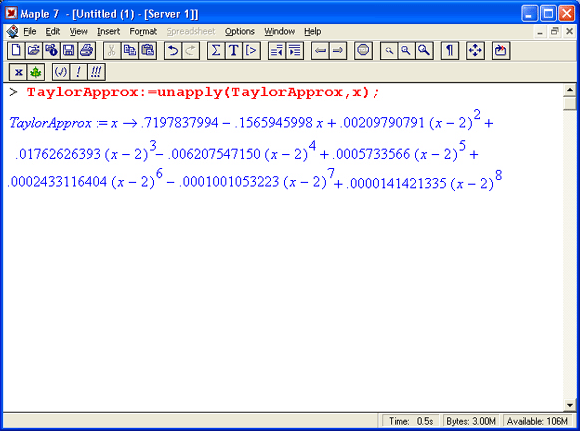
Кривая ошибок для аппроксимации полиномом Тейлора строится командой:
> plotd(f -TaylorApprox,0..4,.color=black);
И имеет вид, представленный на рис. 17.2. Эта кривая нас, прямо скажем, не слишком радует, поскольку погрешность в сотни раз превышает заданную.
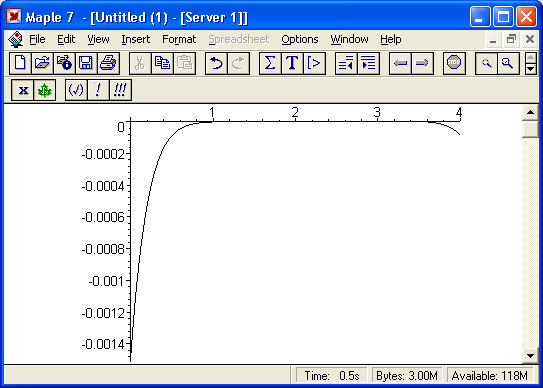
Рис. 17.2. Кривая погрешности при аппроксимации рядом Тейлора
Типичное свойство аппроксимации рядом Тейлора состоит в том, что ошибка мала вблизи точки разложения и велика вдали от нее. В данном случае самая большая ошибка имеет место в левой оконечной точке. Чтобы вычислить значение ошибки в точке х =0, что ведет к делению на нуль (см. определение для f(x)), мы должны использовать значение предела:
> maxTaylorError: = abs(Limit(f(x), х-0) -ТауlorАрргох(0)); maxTaylorError: =. 0015029620
Итак, в самом начале наших попыток мы потерпели полное фиаско. Но отчаиваться не стоит, ибо, как говорят, "даже у хорошей хозяйки первый блин – комом".
