Применение интеграла Дюамеля для расчета переходных процессов
Вернемся к линейным цепям и рассмотрим еще один полезный метод расчета электрических цепей – с помощью интеграла Дюамеля. При нем можно рассчитать временную зависимость выходного напряжения u2(t) цепи по известному входному сигналу u1(t) и переходной характеристике цепи a(t). Возьмем в качестве первого классического примера дифференцирующую RC-цепь и вычислим ее реакцию на экспоненциально нарастающий перепад напряжения.
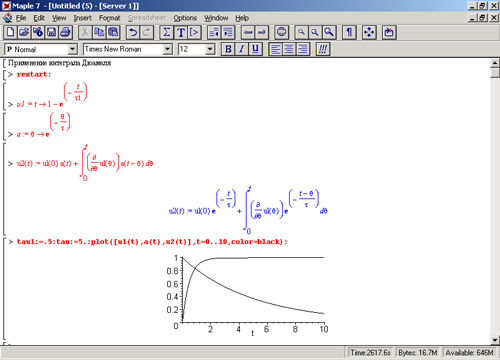
Представлены заданные зависимости u1(t) и a(t), аналитическое выражение для интеграла Дюамеля (одна из 4 форм) и аналитическое выражение для искомой зависимости u2(t). Пока последнее выражение довольно простое. В конце этого фрагмента документа построены графики зависимостей u1(t), a(t) и u2(t).
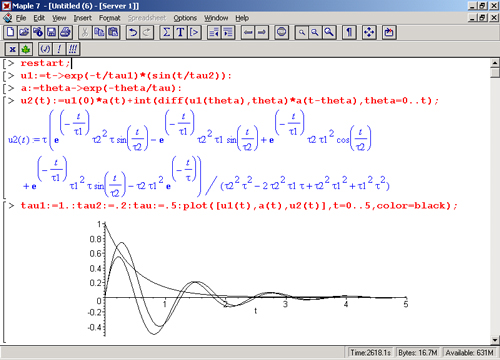
Обратите внимание на то, что выражение для u2(t), получаемое с помощью интеграла Дюамеля, стало намного сложнее. Тем не менее получено как аналитическое выражение для реакции цепи u2(t), так и графики u1(t), a(t) и u2(t). Они показаны внизу графика.
Что нового мы узнали?
В этом уроке мы научились:
- Оценивать возможности Maple 7 в решении конкретных прикладных задач.
- Выбирать аппроксимацию для сложной функции по заданной точности.
- Моделировать различные физические явления (полет камня, движение частицы в магнитном поле и др.).
- Моделировать и проектировать различные электронные схемы (усилителя, аналогового и цифрового фильтра, нелинейной цепи на туннельном диоде).
- Применять интеграл Дюамеля для расчета переходных процессов в линейных цепях.
