Моделирование рассеивания альфа-частиц
Одним из фундаментальных доказательств существования ядра у атомов стал опыт с бомбардировкой тонкой фольги из металла альфа-частицами с высокой энергией. Если бы "массивных" ядер не существовало, то альфа-частицы должны были бы спокойно пролетать сквозь тонкую фольгу, практически не отклоняясь. Однако, как физики и ожидали, некоторая часть частиц испытывала сильное отклонение и даже поворачивала назад. Очевидно, что имели место отскоки (упругие столкновения) с малыми, но массивными ядрами металла фольги.
В нашем распоряжении, увы (а может быть и к счастью), нет ускорителя альфа-частиц. Так что мы, не опасаясь облучения и очередной Чернобыльской катастрофы, сможем смоделировать это интереснейшее физическое явление с помощью математической системы Maple 7. Причем спокойно сидя перед своим домашним компьютером и глубокомысленно наблюдая за траекториями полета альфа- частиц.
Итак, пусть в нашем теоретическом опыте альфа-частицы с энергией 4 МэВ рассеиваются тонкой золотой фольгой. Рассчитать траекторию частицы, приближающейся к ядру атома Аu. Прицельное расстояние р равно 2*10-15 м. Приступим к решению задачи и зададим вначале систему дифференциальных уравнений для траектории альфа-частицы:
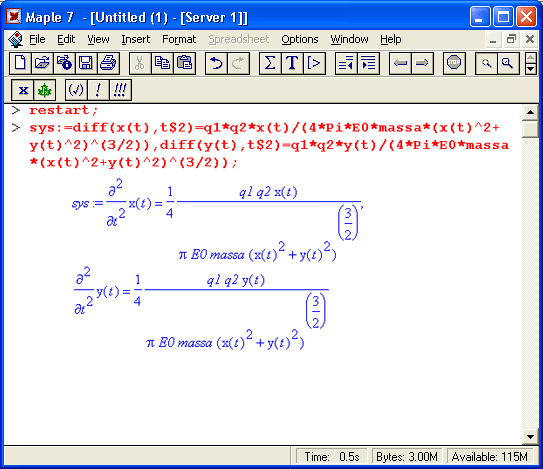
Введем исходные числовые данные для вычислений:
> ql: = 2*i;6e-19:q2: = 79*1.6e-19:massa: = 4*1.67e-27:EO: = 8.85e-12: a: = 4e-13: p: = 5e-15:T: = 4e6*1.6e-19:V0x: = sqrt(2*T/massa):
Создадим графическую структуру решения нашей системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа-частицы от центра ядра атома, находящегося на ее пути:
> with(DEtools):ss: = DEplot({sys},{y(t),x(t)},t=0..7e-20.
[[x(0)=-a,D(x)(0)=VOx,y(0)=p,D(y)(0)=0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*4.D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*8,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*12,D(y)(0)=0].
[x(0)=-a;D(x)(0)=VOx,y(0)=p*16,D(y)(0)=0],
[x(0)-a.D(x)(0)-VOx.y(0)-p*20,D(y)(0)-0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*24,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*28,D(y)(0)=0]],
x(t)=-a..a, scene=[x(t),y(t)],stepsize=le-21.1inecolor=black):
> with(plottools):yy: = circle([0.0],2E-14,color=red,thickness=2):
Warning, the name translate has been redefined
