Паде-аппроксимация
Теперь опробуем рациональную аппроксимацию Паде (Fade) функции f(x) степени (4.4). Приближения по этому разложению будут аппроксимировать функцию более точно, и потому ошибки округления в вычислениях станут более заметными. Поэтому зададим еще два дополнительных знака для точности вычислений.
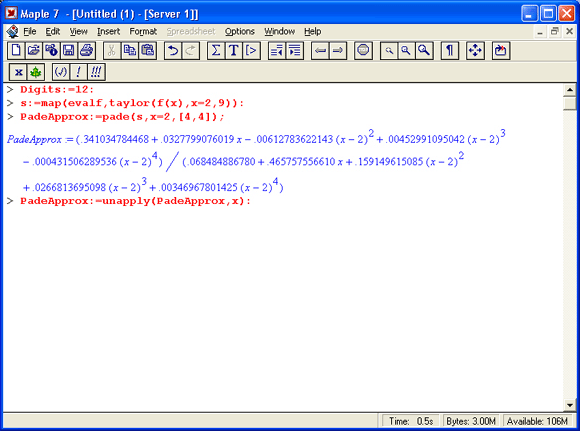
Кривая ошибки для интервала [0, 4] строится командой:
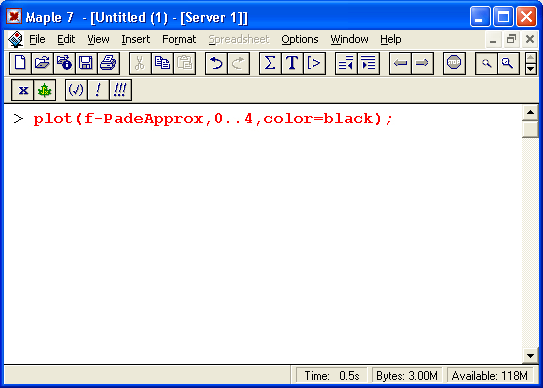
Она имеет вид, показанный на рис. 17.3.
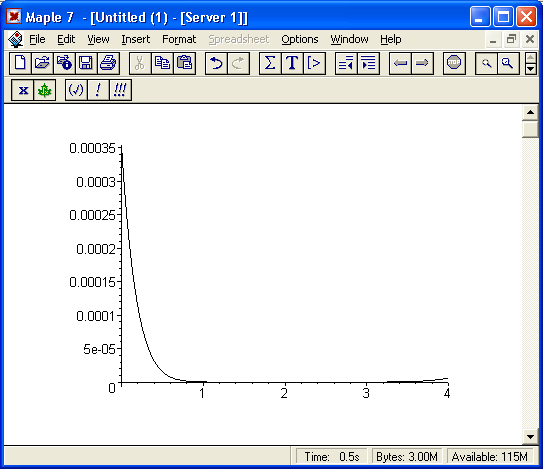
Рис. 17.3. Кривая погрешности при Паде-аппроксимации степени (4.4)
Как и при аппроксимации рядом Тейлора, ошибка здесь мала вблизи точки разложения и велика вдали от нее. Мы снова видим из графика, что для указанной функции, самая большая ошибка – в левой оконечной точке. Однако максимальная ошибка в Паде-аппроксимации уже на порядок меньше, чем при аппроксимации полиномом Тейлора:
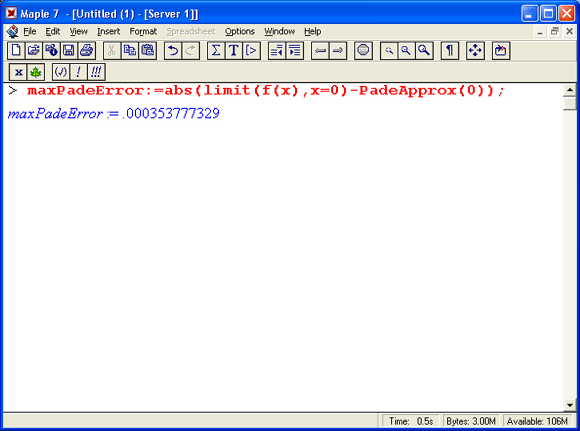
Это успех, показывающий, что мы на верном пути. Но пока погрешность остается слишком большой по сравнению с заданной.
