Аппроксимация полиномами Чебышева
Знатоки техники аппроксимации знают, что лучшие приближения на заданном интервале могут быть получены при использовании разложения в ряд Чебышева. Это связано с тем, что ортогональные полиномы Чебышева позволяют получить аппроксимацию, погрешность которой в заданном диапазоне изменения аргумента распределена более равномерно, чем в предшествующих случаях. Выбросы погрешности на краях интервала аппроксимации в этом случае исключены.
Разложим функцию f(x) на [0, 4] в ряд Чебышева с точностью 1*10-8. Это означает, что все члены с коэффициентами меньше чем эта величина, будут опущены. Такая точность обеспечивается полиномом 13 степени:
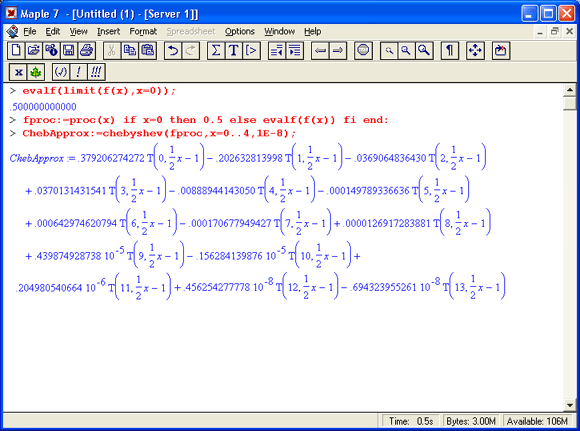
Можно проверить для этого примера, что кривая ошибки при аппроксимации рядом Чебышева колеблется. Поскольку ряд Чебышева был оборван на члене 8-й степени (как и полином ряда Тейлора), то максимальная ошибка оказалась равной приблизительно 0.6* 10-5. Эта величина уже на два порядка меньше, чем ошибка при Паде-аппроксимации, вычисленная выше. Но все же немного не дотягивает до наших требований.
Для последующих вычислений полезно заметить, что мы можем использовать процедуру для нахождения численных значений f(x), которая будет намного эффективнее, чем прямое определение, которое требует численного интегрирования для каждого значениях. А именно определим процедуру численной оценки, основанную на разложении в ряд Чебышева степени 13, так как максимальная ошибка при такой аппроксимации меньше чем 10-8, и обеспечивает для нашей цели достаточную точность.
Мы определим полином Чебышева Т(х) из пакета orthopoly и затем для эффективной оценки преобразуем его в форму Горнера:
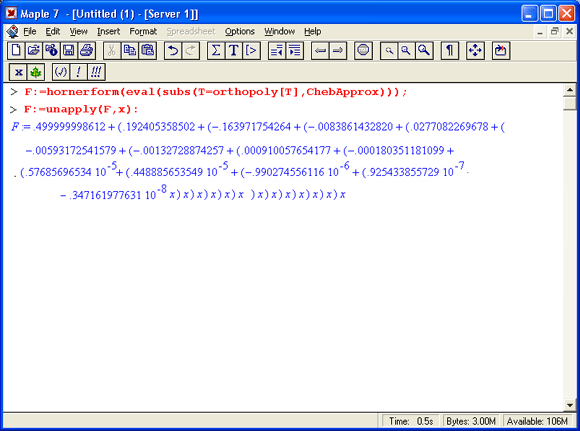
Схема Горнера минимизирует число арифметических операций, заменяя операции возведения в степень операциями последовательного умножения.
