Минимаксная аппроксимация
Классический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (m, n) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax:
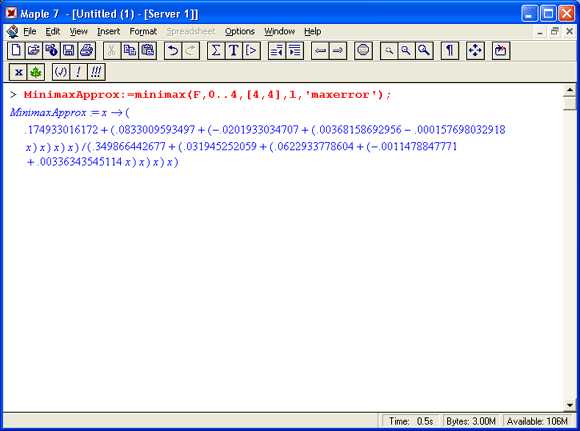
Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы наконец достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10-6:
> maxMinimaxError: = maxerror; maxMinimaxError: =. 585025375366 10-6
Построим график погрешности для данного типа аппроксимации:
> plot(F = MinimaxApprox,0..4,color=black):
График ошибки, представленный на рис. 17.5, показывает равные по амплитуде колебания.
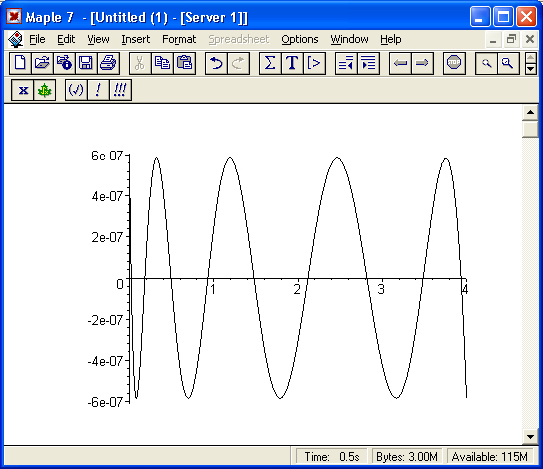
Рис. 17.5. График ошибки при минимаксной аппроксимации
Таким образом, мы добились блестящего успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений.
