Проектирование цифрового фильтра
Вычислим FIR-коэффициенты для прямоугольного окна фильтра:
> С:-=(n) › limit(g,t=n):h: = aray(0..N): N2: = N/2: > for n from 0 to N2 do h[N2-n]: = evalf(C(n)); h[N2+n]: = h[N2-n]; od:
Определим массивы входного x(n) и выходного у(n) сигналов:
> х: = array(-N..T): y: = аrrау(0..Т):
Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:
> for n from -N to -1 do x[n]: = 0; od: > for n from 0 to Т do x[n]: = Dirac(n); od:
Вычислим временную зависимость для выходного сигнала:
> for n from 0 to Т do y[n]: = sum(h[k]*x[n-k],k=0..N): od:
Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:
> р: = [seq([j/fs,y[j]],j=0..T)3: > plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);
Он показан на рис. 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.
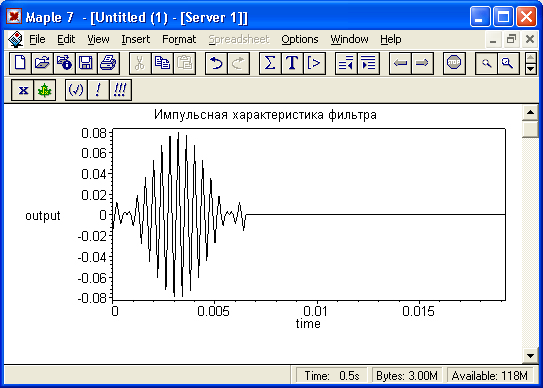
Рис. 17.19. Импульсная характеристика цифрового фильтра
Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:
> rо: = array (1..T+1): io: = arrayd..T+l): > for n from 0 to Т do ro[n+l]: -y[n]; io[n+l]: = 0; od: > FFT(m,ro,io):
Построим график АЧХ фильтра:
> р: = [seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]: > plot(p, frequency=0..fs/2, tabels=[frequency,gain], title='AЧX фильтра',соlоr=black);
Он представлен на рис. 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи – она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).
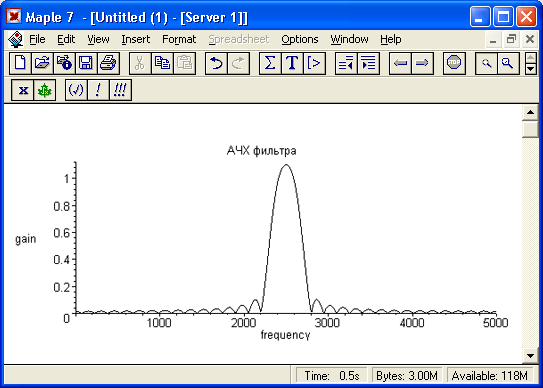
Рис. 17.20. АЧХ цифрового полосового фильтра
