Проектирование цифрового фильтра
Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:
> 1: = round(fs/2/500): > for n from 0 by 2*1 to Т do > for n2 from 0 to 1-1 do > if n+n2 <= Т then > x[n+n2]: = evalf(-l+rand()/10^12-0.5); > fi: > if n+n2+1 <= Т then > x[n+n2-H]:-=evalf(l+ranoX)/10^12-0.5); > fi; > od: > od:
Временная зависимость синтезированного входного сигнала представлена на рис. 17.21.
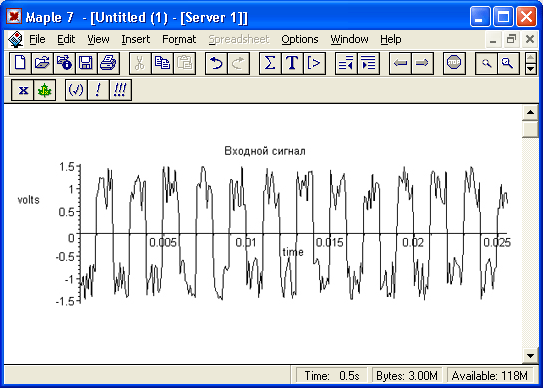
Рис. 17.21. Синтезированный входной сигнал
Вычислим реакцию фильтра на входной сигнал:
> for n from 0 to T do > y[n]: = sum(h[k]*x[n-k],k=0..N); > od:
Построим график выходного сигнала:
> р: = [seq([j/fs, x[j]], j=0..T)]:q: = [seq([j/fs, y[j]], j =0..Т)]: > plot(p,time=0..T/fs/4.labels=[time,volts],title='Входной сигнал",сolor=black); > plot(q,tine=0..T/fs/4.labels=[tirae,volts], titlе='Выходной сигнал",color=black);
Временная зависимость выходного сигнала показана на рис. 17.22. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.
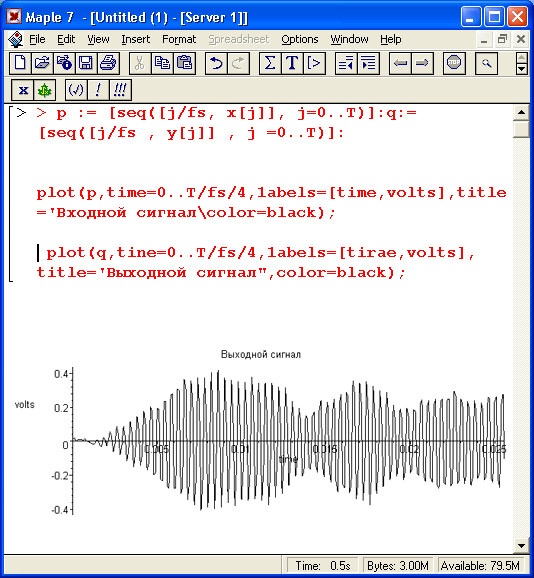
Рис. 17.22. Временная зависимость выходного сигнала цифрового фильтра
