Моделирование цепи на туннельном диоде
Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:
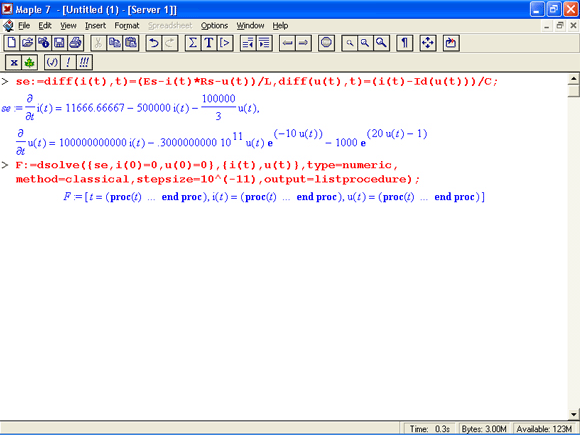
Поскольку заведомо известно, что схема имеет малые значения L и С, мы задали с помощью параметров достаточно малый шаг решения для функции dsolve – stepsize=l(T(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании.
Используя функции odeplot и display пакета plots, построим графики решения в виде временных зависимостей u(t) и 10*i (t) и линии, соответствующей напряжению Es источника питания:
> gu: = odeplot(F,[t,u(t)],0,tm,color=black, labels=['tVu(t),10*i(tr]): > gi: = odeplot(F,[t,10*i(t)],0..tm.color-black): > ge: = odeplot(F,[t,Es].0..tm.color=red):. > display(gu.gi,ge);
Эти зависимости представлены на рис. 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.
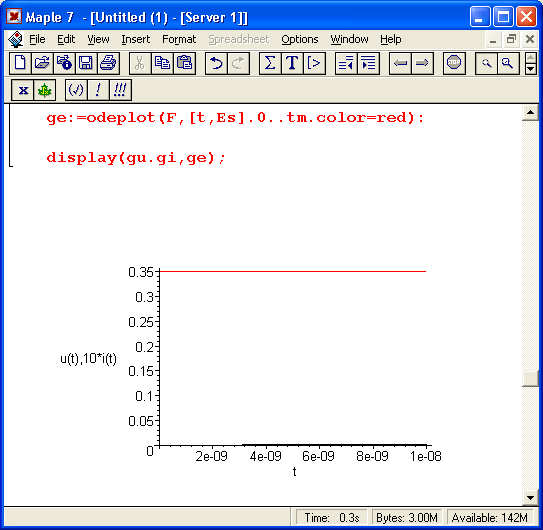
Рис. 17.26. Временные зависимости напряжения на туннельном диоде и тока
