Многочлены
Функция FactorTerms позволяет вынести общий числовой множитель.
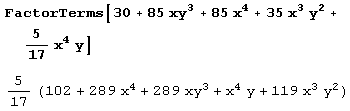
Вызов FactorTerms [poly, x] позволяет вынести общий множитель, не зависящий от х; FactorTerms [poly, {x1, x2,…}] последовательно выделяет множители, не зависящие от x1, х2 и т.д. Вычисление выражения FactorTermsList [poly, (x1, x2,…}] дает список множителей poly. Первый элемент в списке есть общий числовой множитель, второй – множитель, не зависящий ни от одного из x1, х2,…. Последующие элементы есть множители, не зависящие от как можно большего числа переменных x1, х2,….
Деление многочленов
PolynomialQuotient [poly1, poly2] дает частное от деления многочлена poly1 на многочлен poly2, а PolynomialRemainder [poly1, poly2] – остаток.
Наибольший общий делитель многочленов
Важнейшими операциями при работе с полиномами являются нахождение наибольшего общего делителя и наименьшего общего кратного. Выражение PolynomialGCD [poly1, poly2] представляет собой наибольший общий делитель многочленов poly1 и poly2. При вычислении наибольшего общего делителя все символьные параметры в полиномах трактуются как переменные, и деление на них не допускается.
PolynomialGCD[х^3000-1, х^1503-1]
-1 + х3.
Наименьшее общее кратное многочленов
Выражение PolynomialLCM[poly1, poly2] представляет собой наименьшее общее кратное многочленов poly1 и poly2.
Результант
Выражение Resultant [poly1, poly2, var] представляет собой результант многочленов poly1 и poly2, рассматриваемых как многочленов от переменной var.
Resultant[a*x^2+b*x+c, 2a*x+b, x] ab2 + 4 a2 c