Вычисление производных явно заданных функций
Далее осталось только оформить результат (хотя это и не обязательно).
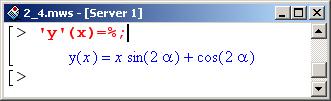
Выражение в левой части заключено в обратные кавычки. Все, что находится в этих кавычках, вычислительным ядром Maple не вычисляется и в области вывода отображается в "первозданном виде". Выше эта особенность была использована, чтобы вывести в области вывода символьное выражение для операции вычисления производной в левой части равенства.
На заметку
Можно для этих целей применять неактивную форму команды дифференцирования Diff {}. Однако в этом случае используется синтаксис как для частной производной, что математически не совсем корректно.
Следует иметь в виду, что для вычисления производной совсем не обязательно сначала описывать саму функцию. Можно поступить проще. Рассмотрим следующий пример (символ ^ означает возведение в степень).
Задача 2.2
Найти производную функции у(х) =х+х^х+х^(х^х).
В этом случае переменной у присвоим значение х+х^х+х^(х^х) (но теперь у – это уже не функция от х, а выражение!).

На заметку
Операция возведения в степень (^ или **) является бинарной. Это значит, что запись вида а^b^с некорректна. Следует использовать скобки: (а^b)^с.
При дифференцировании в качестве первого аргумента процедуры diff () указывается выражение у (зависящее от х, но хочется еще раз подчеркнуть, это не функциональная зависимость) > diff(y,x);
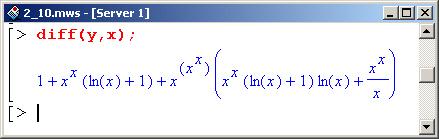
В отличие от предыдущей задачи, зависимость выражения у от х явно не указывается (здесь как раз и проявляется то, что зависимость не является функциональной). В предыдущей задаче переменная у объявлялась как оператор, поэтому при ее вызове необходимо было указать, на какой аргумент она действует. В данном же случае у – это просто название выражения.
Однако самый незатейливый способ вычисления производной представлен ниже.
