Экстремум функции нескольких переменных
Исследование функции нескольких переменных на экстремум отличается от того, что выполняется в случае функции одной переменной. Однако "базовый" принцип все тот же – сначала следует найти точки, в которых производные равны нулю.
На заметку
В случае функции двух переменных/*, у) исследование на экстремум заключается в следующем: сначала находятся точки, в которых производная данной функции равна нулю, а затем составляется матрица размером 2x2 с элементами Ао, которые равны второй производной по i-му и j-му аргументам в точке, где равна нулю производная.
Экстремум имеет место, если определитель матрицы больше нуля. Если диагональные элементы матрицы при этом больше нуля, значит, исследуемая точка – точка минимума. Если диагональные элементы меньше нуля – это точка максимума.
Задача 2.26
Исследовать на экстремум функцию z = х* +у* -х2-2ху -у2.
Задаем функцию z, зависящую от двух переменных х и у.

На следующем этапе нужно решить систему двух уравнений, в которых частные производные от функции z первого порядка приравнены к нулю. Но сначала эту систему (назовем ее SysEq) следует описать.
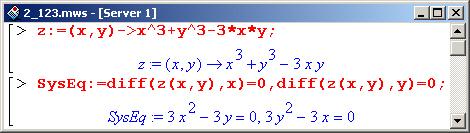
Теперь решаем систему.

В полученном множестве представлено три решения (каждое из которых L также является множеством): первые два действительные, а третье, представленное посредством функции RootOf(), комплексное. Последнее в данном случае интереса не представляет, поэтому его не рассматриваем.
Приведенная ниже процедура вычисляет производную в точке с координатами х и у порядка п по первому аргументу и порядка m по второму аргументу.

Совет
Эту же процедуру можно было определить иначе: F: = (x,у,n,m) › D[n.m] (z) (x,у).
