Экстремум функции нескольких переменных
Детерминант определим следующим образом (переменная Determ).

Внимание!
В данном случае никаких матриц мы не вводили. Но если бы ввели, то элементы матрицы вторых производных определялись через переменные A11, A12 и А22, а детерминант (определитель) матрицы был именно таким, как значение переменной Determ.
Осталось проверить значение переменной Determ в каждой из двух точек (по z).

Детерминант больше нуля, а переменная А11 отрицательна (это был бы диагональный элемент матрицы).
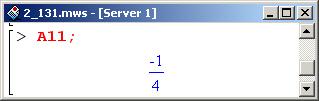
Вывод: исследуемая точка (x=1, y=-1, z=6) – точка максимума. В другой точке имеем следующее.
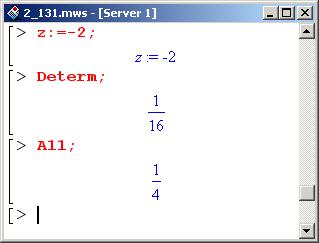
В данном случае получили, что и детерминант, и A11 – больше нуля. Следовательно, точка (x=1, y=-1, z=-2) – точка минимума.
