Частные производные
Для вычисления частных производных применяется процедура diff (). В случае функции нескольких переменных через запятую указываются те из них, по которым берется производная (при этом допускается использование оператора $).
На заметку
Частной производной от функции нескольких переменных называется производная по одной из этих переменных при фиксированных прочих.
При вычислении частных производных допускается также использование оператора D. После оператора в квадратных скобках указывают индекс, соответствующий номеру аргумента функции, по которому вычисляется производная. Например, для функции трех переменных u(x,y,z) производная может быть вычислена с помощью команды D[2.3](u)(x,y,z).
Задача 2.20
Найти частные производные первого и второго порядков от функции и(х,у) = х'+у*-4х2у2.
Определим функцию двух аргументов (аргументы указываются через запятую и заключаются в скобки).

Используя для записи результата процедуру дифференцирования в неактивной форме (Diff ()), вычислим частную производную по х.
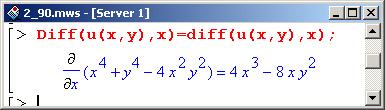
Прочие производные вычисляются аналогично.

Стоит обратить внимание на то, что при вычислении частных производных можно использовать оператор $.

Однако если производных много и они достаточно высокого порядка, запись отдельной команды для каждой такой производной становится утомительным занятием. Иногда в таких случаях полезно определять специальные процедуры, как в следующем примере.
