Экстремум функции
Исследование функции на экстремум подразумевает, как известно, нахождение производной и определение точек, в которых эта производная равна нулю. Далее, по знаку второй производной в найденных точках, определяется тип экстремума – максимум или минимум (если вторая производная меньше нуля – максимум, если больше нуля – минимум).
Задача 2.18
Исследовать на экстремум функцию у(х) = хm (1-х)n.
Сначала определим саму функцию.

Затем найдем ее производную.
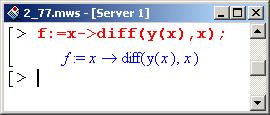
Последняя как несложно проверить, равна следующему.

Выражение можно было бы упростить, но для решения поставленной задачи это не представляется необходимым. Далее определяем точки, в которых производная равна нулю. Воспользуемся процедурой solve(), в качестве параметров которой указываем решаемое уравнение и переменную, относительно которой это уравнение следует решить.
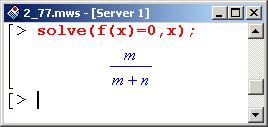
В данном случае экстремум предполагается только в одной точке – в ней производная равна нулю. Это легко проверить. Поступим следующим образом.

Выше переменной х присвоено значение, при котором производная функции должна равняться нулю. Переменная m возвращает значение производной в точке х, а этой переменной только что было присвоено значение.

