Производные высших порядков
Достаточно просто вычисляются и производные высших порядков. Для этого используется все та же процедура diff(). Синтаксис вызова этой процедуры для вычисления производных высших порядков описывается ниже в примерах.
Задача 2.12
Найти у"(х) и у"(х), если y(x) = f(x2).
Для отыскания второй производной можно дважды вызвать процедуру diff (), как показано ниже.
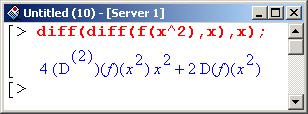
В области вывода оператор D(f) означает производную от функции f() по аргументу, а число в скобках вверху у оператора D определяет порядок такой производной.
Другой подход состоит в том, чтобы использовать оператор формирования последовательности ($) у переменной дифференцирования при вызове процедуры diff ().

На заметку
Таким образом, если после переменной дифференцирования указать оператор $ и целое неотрицательное число, то это число будет определять порядок производной. Подобный подход весьма удобен в тех случаях, когда порядок производной достаточно велик. Поскольку результатом выполнения операции х$3 является последовательность х, х, х, то допустимо вместо $3, например, сразу писать х,х,х – результат от этого не изменится.
Задача 2.13
Найти 100-ю производную функции y(x) = xsh(x).
Опишем дифференцируемую функцию.
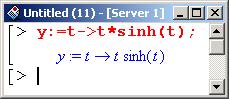
После этого ее можно продифференцировать нужное количество раз.
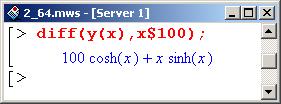
Ситуация несколько усложняется, если функция задана в параметрическом f виде. Как поступать в этих случаях, показано в следующем примере.
