Производные от неявно заданных функций
Задача 2.10
Чему равно значение у' при х = 2 и у = 4 и при х = 2 и у = 0, если x^2/a^2+y^2/b^2=1 (эллипс)?
Для начала задаем уравнение F, определяющее функцию.

Выражение Fx определяет производную. Записывается оно с помощью процедуры implicitdiff(), первым параметром которой указывается дифференцируемое выражение (F), затем следует переменная, которую при дифференцировании следует считать функцией, и, наконец, переменная, по которой вычисляется производная.

Переменным х и у присваиваем следующие значения.

Если теперь вызвать Fx, то в этом выражении х и у будут заменены значениями, присвоенными этим переменным выше. В этом случае получим значение производной в соответствующей точке. Однако вызвать Fx можно и с помощью переменной среды %%%, которая возвращает значение предпредпоследней операции.

Чтобы вычислить производную в другой точке, переменной у следует присвоить новое значение (переменная х значения в новой точке не меняет).

Однако результат несколько неожиданный.
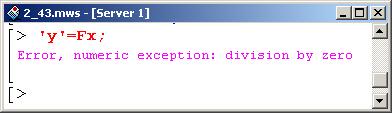
Дело в том, что производной в этой точке не существует (точнее, она равна бесконечности, поскольку в выражении для производной у находится в знаменателе, и поэтому точка у=0 является особой).
Часто уравнение, которое задает неявно функцию, имеет достаточно специфичный вид – например, может быть записано в полярных координатах.
