Вычисление производных явно заданных функций
Задача 2.6
Найти производную и построить график функции и ее производной, если:
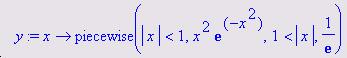
Исходную функцию определяем следующим образом (процедура abs () возвращает в качестве значения модуль аргумента).
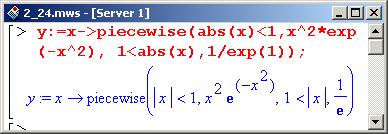
Однако производную определим не как функцию, а как выражение.

Видим, что производная не определена в точках х=-1 и х=1 (undefined – значит неопределенный). Ниже строится график исходной функции и ее производной. Следует обратить внимание на то, что оператор у() указывается вместе с аргументом (т.е. у(х)), в то время как для производной указана только переменная f. Ситуация такая же, как и в одном из предыдущих примеров, – первая зависимость от х является функциональной (у() – оператор), вторая – нет (f – это выражение).
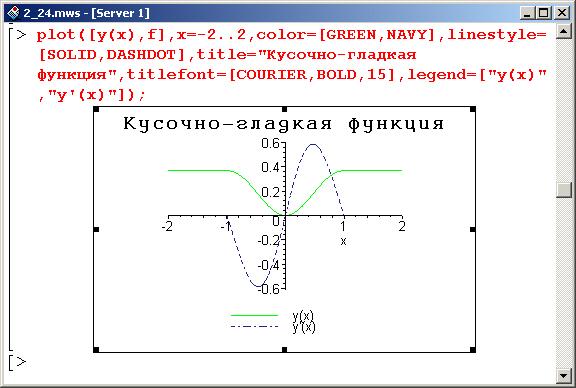
Опция linestyle определяет стиль линий: первый график отображается сплошной линией (SOLID), второй – штрихпунктирной (DASHDOT).
