Вычисление производных явно заданных функций
Задача 2.3
Найти производную функции у(х)=х^(1/х).
В качестве параметра процедуры diff () можно сразу указать дифференцируемое выражение.

Поскольку очевидно, что в полученном после дифференцирования выражении имеется возможность вынести за скобки общий множитель, воспользуемся следующей командой.

Переменная среды %, указанная в качестве первого параметра процедуры collect(), определяет выражение, которое нужно преобразовать, а второй параметр указывает на то, что в выражении слагаемые следует группировать по степеням 1/х.
На заметку
Если при вызове процедуры collect() вторым параметром указать не 1/х, а х, результат не изменится. Причина в том, что 1/х – это х в степени -1.
Вычислительное ядро Maple достаточно эффективно работает не только с непрерывными функциями, но и с такими, которые имеют точки (или области) разрывов.
Задача 2.4
Найти производную функции 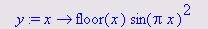 .
.
Определяем функцию у(х) следующим образом.

При этом целая часть числа х возвращается функцией Maple floor().
На заметку
В Maple есть функция trune(), действие которой во многом аналогично действию функции floor(). Однако функция trunc() выделяет целую часть аргумента "в направлении О", в то время как функция floor () выделяет ближайшее целое число, не превышающее данное, указанное как аргумент. Для положительных чисел действия обеих функций эквивалентны, а для отрицательных чисел результаты отличаются на единицу.
