Производные высших порядков
Задача 2.14
Найти y(x), если x(t) = 2t-t2 и y(i) = 3t-t3.
Вначале определим параметрические зависимости для х и у (т.е. объявим эти переменные как функции одного параметра).
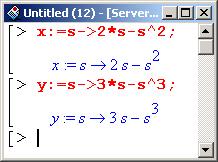
Теперь определим процедуру paramdiff() (точнее, оператор, т.е. в качестве результата процедурой возвращается действие), параметрами которой являются две функции (у() и х()). Действие данного оператора на аргумент состоит в вычислении параметрической производной от функции, указанной первым параметром оператора, по второй. Переменной-параметром при этом является аргумент, на который действует оператор paramdiff(). Описание процедуры заканчивается точкой с запятой, поэтому в области вывода можно увидеть сгенерированный для процедуры программный код.
На заметку
Чтобы этот код не отображался, в конце процедуры достаточно поставить двоеточие.

В процедуре описана локальная переменная t, которая доступна только внутри тела процедуры. Далее следует команда, определяющая работу процедуры paramdiff (). Согласно этой команде, переменной t в соответствие ставится (›) параметрическая производная от у по х (diff (y(t),t)/diff (x(t),t)), а сама переменная t при этом является параметром.
Теперь можно вычислить первую производную.

На заметку
То, что в предыдущей команде при вызове paramdiff () в качестве аргумента указана переменная t, которая формально идентична локальной переменной в описании этой процедуры, – простое совпадение. Можно было бы указать и иной параметр, например р или v.
