Экстремум функции нескольких переменных
Задача 2.28
Найти точки условного экстремума функции и = хг +/, если х/а+у/b = 1.
Это задача на условный экстремум, и решать ее будем методом неопределенных множителей Лагранжа.
Вводим функцию z, которая, помимо х и у, зависит еще и от параметра А.

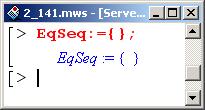
Инициализируем переменную-множество EqSeq для записи в нее в последующем уравнений, определяющих точки возможного экстремума.
На следующем этапе заполняем это множество уравнениями. Каждое такое уравнение – приравненная к нулю производная по одной из переменных х, у или по параметру λ. Весь процесс автоматизирован посредством использования оператора цикла for.

В рамках этого оператора при помощи переменной t перебираются все параметры, по которым берется производная, сама производная приравнивается к нулю, а уравнение записывается с помощью оператора объединения множеств union в переменную EqSeq.
В результате получаем следующую систему уравнений (она записана в переменной EqSeq в виде множества уравнений).

Теперь эту систему решаем.

