Экстремум функции нескольких переменных
Снова разбиваем уравнение на операнды.

Теперь само уравнение используем для того, чтобы связать между собой дифференциалы dx и dy.

Дифференциал dy выражаем через dx.

Полный дифференциал тогда равен следующему.
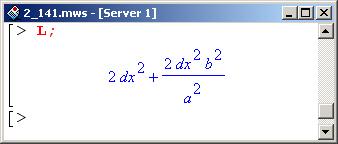
Группируем слагаемые при dx, в результате чего получим:

Определяем знак этого выражения.
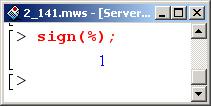
Таким образом, приходим к выводу, что функция имеет условный минимум.
