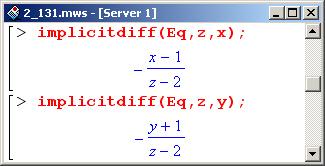
Экстремум функции нескольких переменных
Матрица А – это матрица вторых производных исследуемой на экстремум функции в первой точке предполагаемого экстремума, в то время как матрица В – во второй точке.

Чтобы выяснить, являются ли исследуемые точки экстремальными, нужно вычислить детерминанты определенных выше матриц. В пакете linalg для этих целей предусмотрена процедура det(), которую можно вызвать следующим образом.
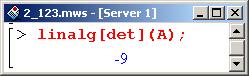
Поскольку детерминант меньше нуля, то в первой точке экстремума нет. Ниже показано, как вызвать все ту же процедуру, но с несколько иным синтаксисом (сначала подключается пакет).
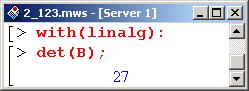
Здесь детерминант больше нуля. Следовательно, вторая точка является точкой экстремума.
Внимание!
В Maple 9 процедуры пакета linalg распределены по пакетам LinearAlgebra и VectorCalculus. Однако на пакет linalg можно по-прежнему ссылаться, что и было сделано выше.
Необходимо определить знак первого диагонального элемента матрицы (знак другого диагонального элемента будет таким же).
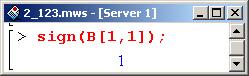
Поскольку этот элемент больше нуля, приходим к выводу, что точка (х=1, у=1) является точкой минимума.
На заметку
Ссылка на элемент матрицы в выполняется в виде В[ i, j ], где i и j – индексы вызываемого элемента.
Задача 2.27
Найти экстремальное значение неявно заданной функции z от переменных х и у, если хг+у2 +z* -2x -2y-4z-10 = 0.
В данном случае имеем дело с неявно заданной функцией. Вначале запишем уравнение.

После этого достаточно просто вычислить частные производные от z по х и у.