Процедуры пакета CurveFitting
Теперь по базовым точкам выполним аппроксимацию. Сначала воспользуемся линейной зависимостью, предлагаемой по умолчанию.
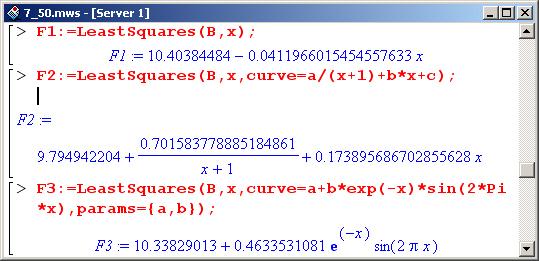
В пределах погрешности, с которой определялись базовые точки, параметры определены совсем не плохо.
Внимание!
Выше при вызове процедуры LeastSquares() обязательно следует указывать значение для опции params. Если этого не сделать, то константа Pi в аргументе синуса будет интерпретироваться как параметр оптимизации. Поскольку функция по параметру нелинейна, ничем хорошим это не закончится (появится сообщение об ошибке).
Построим графики для полученных зависимостей. Вместе с графиками квадратами отобразим точки, по которым выполнялась оптимизация.
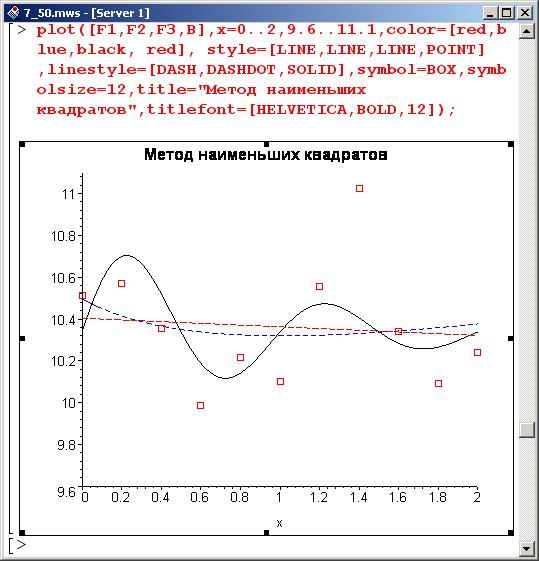
Первые две штрихованные кривые мало чем отличаются, в то время как третья (сплошная линия) достаточно точно отображает исходную зависимость. Однако чтобы в общем случае методом наименьших квадратов эффективно строить аппроксимирующие функции, необходимо знать вид аппроксимируемой функциональной зависимости.
