Численное дифференцирование
С учетом начального условия решим данное уравнение в численном виде (решать уравнение в численном виде без начальных условий крайне проблематично).

Прежде чем появится результат, выводится сообщение, гласящее буквально следующее: "Внимание, невозможно определить значение далее. 96981062, возможна сингулярность". Поэтому значения функции будем определять только на интервале от 0 до указанного выше значения. Для того, чтобы вычислить значение функции в точке, следует указать эту точку аргументом определенной выше процедуры nsol().
Например, значение в нуле вычисляется так.

На заметку
В данном случае в результате выполнения команды nsol(0) выводится список, в котором указано значение точки и значение функции в этой точке. В общем случае в таком списке присутствует еще и значение для всех производных вплоть до порядка, на единицу меньшего порядка старшей производной в решаемом уравнении. Поскольку старшей производной в данном уравнении является производная первого порядка, в списке представлены только точка и значение функции в этой точке.
Выведем численные значения функции на интервале от 0.1 до 0.8 с шагом 0.1. Результат представлен ниже.
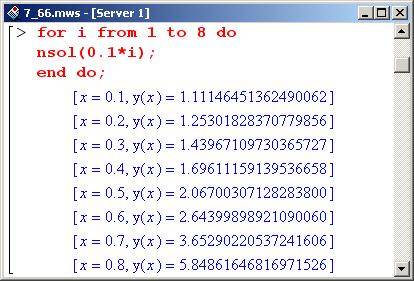
Сами по себе эти значения мало о чем говорят. Интересно их сравнить с точным решением уравнения. Maple с такой задачей справляется, однако результат довольно громоздок. Нас интересуют значения функции только в некоторых точках, причем значения эти, чтобы их можно было сравнивать, должны быть в формате чисел с плавающей точкой. Поэтому поступим следующим образом: решим уравнение, а к полученному результату применим операцию выделения функциональной зависимости unapply(). Результат присвоим переменной f, но выводить на экран его не будем.

Внимание!
Результатом решения уравнения является, как известно, равенство. Если процедуру unapply() применить к равенству, то получим оператор, действие которого на аргумент состоит в восстановлении равенства, правда, уже с переменной, указанной аргументом оператора. Это замечание важно для понимания результата выполнения команд, приведенных ниже.
