Численное интегрирование
Рассмотрим примеры, в которых интегралы вычисляются разными методами. Для начала вычислим следующий интеграл.

Если интеграл вычислять адаптивным 30-точечным методом Гаусса, результат получится таким же.

Далее рассмотрим интеграл от функции, имеющей особенность на границе интегрирования.
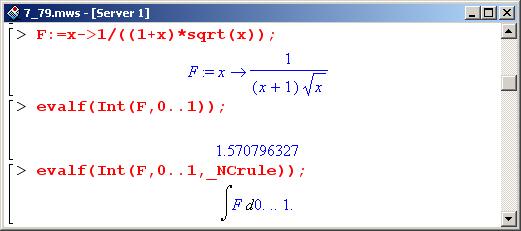
Внимание!
Явное указание метода интегрирования автоматически означает, что никакие другие методы, в том числе и методы обработки сингулярностей, не используются.
Наконец, с помощью двойного интеграла вычислим площадь круга единичного радиуса.

В Maple 9 воспользоваться приведенной выше командой не удастся из-за переопределения опции для метода Монте-Карло и изменения синтаксиса вызова команд вычисления многократных интегралов. В качестве утешения можно посчитать площадь квадрата.

На заметку
Вычисление интегралов методом Монте-Карло основано на использовании вероятностных оценок. Например, площадь круга могла бы вычисляться так: генератором случайных чисел продуцируются точки на плоскости, попадающие во внутреннюю область квадрата с координатами вершин (1.1), (-1.1), (-1,-1), (1,-1). Затем среди этих точек подсчитывается (в процентном отношении) количество тех, которые попадают во внутреннюю область круга единичного радиуса, вписанного в этот квадрат. При большом количестве точек упомянутое процентное отношение будет одновременно определять отношение площади круга к площади квадрата. Последняя, очевидно, равна 4. Метод достаточно элегантный, но не очень точный.
Вывод, как и в случае численного дифференцирования, состоит в том, что спецификацию метода разумно выполнять только в тех случаях, когда пользователь полностью уверен в правильности своих действий.
