Работа со списками и массивами. Списки и их свойства.
Списки относятся к данным множественного типа. Они имеют большое значение при обработке массивов данных и служат основой для создания векторов и матриц. В этом разделе мы познакомимся со свойствами списков, их созданием (генерацией) и использованием.
Часто математические или иные объекты содержат множество данных, которые желательно объединять под общим именем. Например, под объектом с именем М можно подразумевать квадратную матрицу размером 10x10 с общим числом элементов, равным 100. Человека с именем Victor, например, можно характеризовать целым списком разных данных – символьными фамилией, именем и отчеством, целочисленным годом рождения, вещественным ростом, объемом груди и т. д.
Для объединения данных могут использоваться списки (list). Mathematica имеет обширные возможности работы с объектами-списками, содержащими не только однотипные, но и разнотипные элементы. В частности, элементами списков могут быть числа, константы, переменные, выражения и даже сами списки. Списки используются для конструирования более частных типов данных – массивов, матриц и векторов [87].
На языке данной системы список – это совокупность произвольных данных, указанных в фигурных скобках, например:
{1, 4, 2, 7, 9} или {a, b, c, d, e, sin[x], ln[y], "string"}Возможно задание списков в списке, например, так:
{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}Такой список представляет матрицу:
1 2 34 5 67 8 9Однако, чтобы вывести список в такой матричной форме, надо использовать после списка выражение //MatrixForm (рис. 3.7).
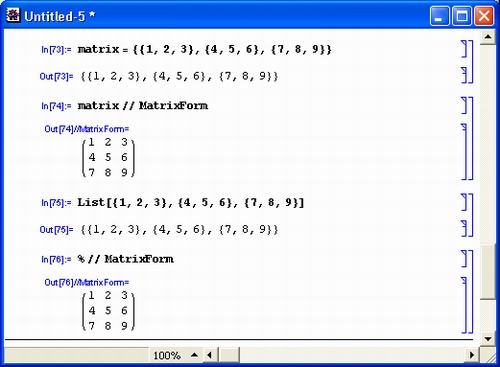
Рис. 3.7. Примеры задания и вывода матрицы
На рис. 3.7 показан еще один способ задания списка или матрицы – с помощью функции List:
- List [a, b, с,…] – создает список {а, b,, с,…};
- List [ {а,b, с,…}, {d,e, f,…}, {i, k, 1,…} ] – создает список – матрицу { {a,b, с,…}, {d,e, f,…}, {i, k, 1,…} }.
Списки можно составлять, непосредственно задавая объекты в соответствии с описанным синтаксисом. Однако можно и генерировать некоторые виды списков, таких как таблицы. Списки могут быть объектами присваивания переменным, например:
V := {1, 2, 3, 4, 5}Списки характеризуются размером, который представляет собой произведение числа элементов списков по каждому направлению (размерности). Например, одномерный список является вектором и характеризуется числом элементов по единственному направлению. При этом вектор может быть вектором-строкой или вектором-столбцом. Двумерный список представляет матрицу, имеющую m строк и n столбцов. Ее размер равен mxn. Если m=n, то матрица называется квадратной. Трехмерный список можно представить в виде параллелепипеда, содержащего mxnxp элементов. Списки большей размерности трудно наглядно представить, но они вполне возможны. Напомним, что имена векторов и матриц в данной книге обозначены жирными символами, например, V для вектора и М для матрицы.
