Функции линейной алгебры
Следующая группа функций системы Mathematica позволяет осуществлять над векторами и матрицами основные операции, используемые в линейной алгебре:
- Cross [vl,v2, v3,…] – векторное произведение (может задаваться в виде v1*v2*v3*…);
- Det [m] – возвращает детерминант (определитель) квадратной матрицы m;
- DiagonalMatrix [list] – возвращает диагональную матрицу с главной диагональю, сформированной из элементов списка list, и нулевыми остальными элементами матрицы;
- Dot [a, b, с] – возвращает произведения векторов, матриц и тензоров. Операцию произведения можно задавать также в виде а .b. с;
- Eigensystem[m] – возвращает список {values, vectors} собственных значений и собственных векторов квадратной матрицы т;
- Eigenvalues [m] – возвращает список собственных значений квадратной матрицы m;
- Eigenvectors [m] – возвращает список собственных векторов квадратной матрицы m;
- IdentityMatrix [n] – возвращает единичную матрицу размером пхп (у нее диагональные элементы имеют значения 1, остальные 0);
- Inverse [m] – возвращает обратную матрицу для квадратной матрицы т, то есть матрицу m-1, которая, будучи умноженной на исходную матрицу, дает единичную матрицу;
- LinearSolve [m, b] – возвращает вектор х, представляющий собой решение матричного уравнения m .x==b, где m – матрица коэффициентов левой части системы линейных уравнений, х – вектор неизвестных и b – вектор свободных членов в правой части системы;
- Tr [list] – возвращает след матрицы или тензора (эта функция есть только у Mathematica 4);
- Transpose [m] – возвращает транспонированную матрицу, у которой столбцы и строки меняются местами в сравнении – с исходной матрицей m;
- RowReduce [m] – производит гауссовское исключение переменных, возвращая упрощенную форму матрицы m, полученную путем линейного комбинирования строк.
Следующие примеры иллюстрируют применение основных из этих функций.
| Ввод (In) | Вывод (Out) |
|---|---|
| A: =IdentityMatrix [3] А |
{{1.0,0},{0, 1, 0}, {0, 0, 1}} |
| MatrixExp [A] | {{E,0,0},{0, E, 0}, {0, 0, E}} |
| MatrixQ [A] | True |
| MatrixPower [MatrixExp [A], – 1. 5] | {{0. {0.22313, 0, 0}, {0, 0.22313, 0), 0, 0.22313}} |
| А+{{1.2.3},{4.5.6},{7.8.9}} m: = {{1.2},{3.7}} |
{{2.2,3},{4, 6, 6}, {7, 8, 10}} |
| Inverse [m] | {{7,-2}, (-3, 1}} |
| MatrixQ [m] | True |
| RowReduce [m] | {{1.0},{0, 1}} |
Вычисление детерминанта матрицы и функций, относящихся к собственным значениям, представлено на рис. 3.11.
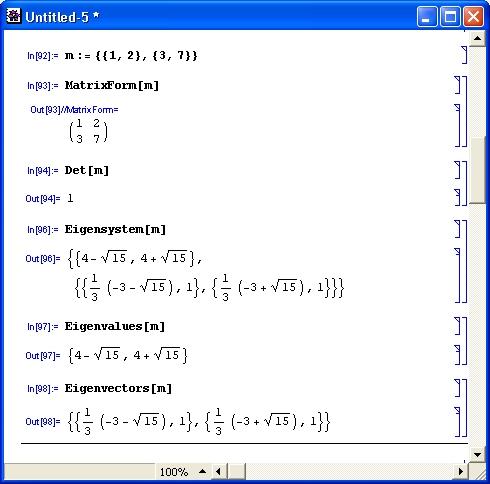
Рис. 3.11. Вычисление детерминанта, собственных значений и векторов матрицы
Приведем еще несколько примеров:
m={{1, 2}, {3, 7}} {{1, 2}, {3, 7}} Transpose[m] {{1, 3), {2, 7}} m//MatrixForm 1 23 7 Transpose[m]//MatrixForm Inverse[m]//MatrixForm 7 -2-3 1В приложении указан ряд дополнительных матричных функций, применяемых реже, чем описанные выше функции.
