Что такое число
Что такое число? Однозначного ответа на этот вопрос нет. Например, комплексное число – это число или все-таки вектор? А действительное число – это число или сечение во множестве рациональных чисел? А если комплексные числа все-таки числа, то кватернионы – тоже числа или уже объекты другой природы? Ну а если даже кватернионы – все-таки числа, то разве не следует к числам причислить и октавы Кэли? Иногда очень удобно считать, что числа – это элементы любого кольца. Но тогда и матрицы (элементы кольца матриц) тоже ведь нужно считать числами! Впрочем, это совсем не глупо, как может показаться на первый взгляд: в кольце матриц размера 2x2, элементами которых являются вещественные числа, можно выделить подкольцо, которое на самом деле является полем, изоморфным полю комплексных чисел. Так что не удивительно, что каждая эпоха в истории математики давала свой ответ на вопрос о том, что такое число.
Не удивительно и то, что в системе Mathematica предусмотрено несколько типов чисел. В качестве базовых типов чисел удобно рассматривать целые, рациональные, вещественные и комплексные числа. Все они могут содержать практически любое количество цифр. (Все же количество цифр, конечно, ограничено объемом имеющейся памяти.)
Чтобы разобраться в этом, давайте рассмотрим классический пример – занимательную задачу из многих популярных книг по математике для младших школьников.
Пример 3.1
Наибольшее число, которое можно записать тремя цифрами. Постановка задачи: какое наибольшее число можно записать с помощью трех цифр?
Ну, конечно, 999, почти не задумываясь, отвечают школьники. И знаете, они по-своему правы. Ведь поскольку в условии задачи говорится о цифрах, то их можно только записывать одна за другой. Поскольку их три, значит, число будет трехзначным. А 999 – наибольшее трехзначное число, причем в его записи используется только три девятки. Но оказывается, что не все так просто. Ведь на самом деле постановка задачи нечеткая. Действительно, в условии ведь не указано, как три цифры можно использовать для записи числа. Ведь каждую из трех цифр можно использовать для записи чисел, а затем над этими числами выполнить какие-нибудь операции. Можно, например, с помощью двух цифр записать число 99, а с помощью оставшейся цифры – число 9, а затем возвести 99 в степень 9: 99".
С вычислением этого числа система Mathematica справляется без малейших затруднений.
999 = 913517247483640899.
Но можно числа 9 и 99 скомбинировать и иначе: 999. Система Mathematica без труда вычислит и это число.
999 = 295126654306527521487534802261977363143592725
17043832886063884637676943433478020332709411004889.
Мы сразу видим, что 9" гораздо больше, чем 999. Но вот тут-то оказывается, что есть еще и третий вариант: 99'. Это число имеет 369 693 100 цифр, т.е. более трети миллиарда! Понятно, что во многих компьютерах объем памяти меньше количества цифр этого числа, и потому система Mathematica записать его не сможет. (Если вы все же решили вычислить это число и вам надоело ждать, выберите Ядро › Прервать вычисление.)
Впрочем, если допустить еще и операцию вычисления факториала, то, так как 9! = 362880, с помощью трех цифр можно записать еще большее число: 9??. Это число система Mathematica уж точно записать не сможет! Правда, вычислить показатель степени – число 99!, десятичная запись которого содержит 65 269 цифр, системе Mathematica вполне под силу!
Наконец, замечу, что авторы популярных книжек упустили еще одну возможность: использование скобок. С их помощью (и факториала), даже одной девятки (или любой другой цифры, большей 2), можно выписать бесконечно возрастающую последовательность чисел.
9, 9! = 362880, (9!)!, ((9!)!)!, (((9!)!)!)!, ((((9!)!)!)!)!,…
Уже число (9!)! содержит 4 282 655 цифр, но система Mathematica справляется и с ним! Но вот предложить ей вычислить следующее число в этой последовательности даже и не пытайтесь!
Разобравшись немного с числами, давайте изучим операции над ними. Как видно из примера, арифметические операции над целыми и рациональными числами, как и во многих других системах компьютерной алгебры, выполняются точно (все цифры результата верные). Вот, например, результат возведения в сотую степень числа пять, найденный системой Mathematica.
5100 = 7888609052210118054117285652827862
29673206435109023004770278930640625.
Однако при таком представлении целых или рациональных чисел иногда трудно судить о величине результата. Кроме того, поскольку система Mathematica стремится сохранить точность, она оставляет фактически невычисленными такие выражения, как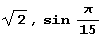 
.
Поэтому вполне логично задать вопрос: как же сделать так, чтобы система Mathematica производила вычисления над вещественными числами, представляя результаты в виде десятичных дробей с заданным количеством разрядов?