Периодические цепные дроби
Как доказал Лагранж, все квадратичные иррациональности (и только они) разлагаются в периодические цепные дроби. Как учитывает это обстоятельство система Mathematica? Давайте выясним это на примере разложения квадратных корней из чисел начального отрезка натурального ряда, деленных на 1, 2, 3. Вот определение нужных нам функций.
Fn01[n_] := Sqrt[n] Fn02[n_] := Sqrt[n] / 2Fn03[n_] := Sqrt[n] / 3Теперь можем написать программу.
Do[Print[n, ": ", ContinuedFraction[Fn01[n]], ":", ContinuedFraction[Fn02[n]], ":", ContinuedFraction[Fn03[n]]], {n, 1.100} ]Результаты отформатируем в виде таблицы.
Эта таблица заслуживает того, чтобы рассмотреть ее более внимательно. Многие приведенные в таблице квадратичные иррациональности имеют вид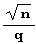 
причем n2 >q. Во-первых, период цепной дроби, представляющей такую квадратичную иррациональность, начинается сразу после целой части. (Это следует из теоремы о чисто периодических цепных дробях, которую Эварист Галуа опубликовал в 1828 году.)
Во-вторых, последний элемент периода равен удвоенной целой части. (Это следует из доказанной Эваристом Галуа теоремы о том, что в случае чисто периодического разложения сопряженная квадратичная иррациональность имеет те же элементы, но расположены они в обратном порядке.)
Наконец, давайте посмотрим, как в системе Mathematica представляются чисто периодические разложения.
ContinuedFractiont(1 + 13 ^ (1 / 2)) / 3] {1, {1.1.6.1.1}}Сюрприз! Целая часть, как видите, выделена отдельно, а период записан только со следующего звена! Во многих учебниках по теории чисел считается, что период начинается с первого звена и потому вся дробь записывается в виде {{1.1,1.6.1}}. Конечно, здесь различие только внешнее, но его следует иметь в виду, сравнивая результаты, полученные с помощью системы Mathematica, с результатами, полученными другими системами. Впрочем, при разложении чисел в цепные дроби могут происходить и более серьезные неожиданности…