Частные случаи разложения чисел в цепные дроби
Составим теперь таблицу разложения квадратичных иррациональностей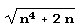 
и 
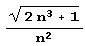в цепные дроби.
Вот определения нужных нам функций.
Fn1[n_] := Sqrt[n ^ 4 + 2n] Fn2[n_] := Sqrt[2n ^ 3 + 1] / 2Программа может быть такой.
Do[Print[n, ":", ContinuedFraction[Fn1[n]], ":", ContinuedFraction[Fn2[n]]], {n, 1.100} ]По результатам выполнения программы составляем таблицу. Обратите внимание на третий столбец этой таблицы. Вы увидите, что длина периода некоторых дробей вида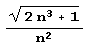 
очень быстро увеличивается с ростом и, причем рядом с дробями, имеющими очень короткий период, соседствуют дроби, длина периода которых весьма значительна.
Составим теперь таблицу разложения квадратичных иррациональностей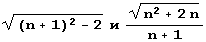 
в цепные дроби. Вот определения нужных нам функций.
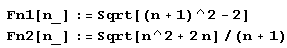
Программу можно не менять; результат выполнения ее представлен в табл. Б.7.
Интересно отметить, что хотя квадратичная иррациональность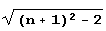 
выглядит проще, чем квадратичная иррациональность 
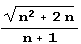ее период в два раза длиннее.
Более того, в разложении квадратичной иррациональности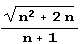 
в цепную дробь лишь первый элемент периода зависит от n.
Чтобы составить таблицу разложения квадратичных иррациональносте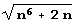й 
и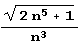 
в цепные дроби, нужно дать лишь новые определения нужным нам функциям.
Fn1[n_] := Sqrt[n ^ 6 + 2n] Fn2[n_] := Sqrt[2n ^ 5 + 1] / (n ^ 3)Обратите внимание на то, что у заурядной иррациональности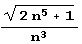 
период может быть и довольно коротким (что случается редко) и невероятно длинным! При п = 9 он содержит 69 950 элементов! Кто бы мог подумать, что разложение вполне заурядного числа 
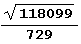в цепную дробь имеет такой длинный период! Квадратный корень сам по себе, между прочим, в длине периода не виноват, поскольку период разложения 
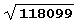содержит всего лишь 266 элементов.
Составим, наконец, таблицу разложения в цепные дроби квадратичных иррациональностей: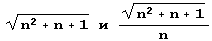 
Для этого дадим определения нужным нам функциям.
Fn1[n_] := Sqrt[n ^ 2 + n + 1] Fn2[n_] := Sqrt[n ^ 2 + n + 1] / nПосле выполнения программы составляем таблицу. Обратите внимание на второй столбец этой таблицы. Вы увидите, что вполне заурядная иррациональность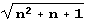 
(квадратный корень из простенького квадратного трехчлена) имеет разложение в цепную дробь, период которой подчас длиннее, чем того можно было бы ожидать. Но куда большую неожиданность в этом смысле "подбрасывает" дробь 
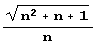отличающаяся всего лишь наличием простенького знаменателя!