Трудные случаи при разложении чисел в цепные дроби
Это указывает на то, что в системе Mathematica первое звено цепной дроби не всегда равно целой части числа, даже если число положительно. Во-вторых, оба звена в периоде отрицательны. Все это может усложнить восприятие числа и никоим образом не одобряется авторами учебников и задачников по теории чисел. Такое представление не является стандартным, и потому будьте внимательны. А вот пример стандартного представления:
А вот и еще один пример. Попытаемся разложить целое число 40= Sgrt[57-40Sqrt[2]]-Sqrt[57+40Sqrt[2]] В цепную дробь.
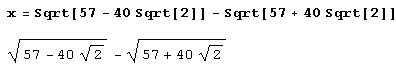
Результат вообще абсурдный:
Заметьте, утверждается, что дробь не является ни конечной, ни периодической! Против отсутствия периода я бы не спорил, но звеньев-то всего одно! Если же указать фактическое количество звеньев, результат получить все равно не удастся.
Фокус с увеличением количества звеньев (например, до миллиона) здесь не проходит, поскольку трудности возникают уже при вычислении целой части, т.е. первого звена.
Мы разобрали всего лишь несколько примеров, где поведение системы Mathematica, мягко скажем, слабо предсказуемо.
Но, надеюсь, вы понимаете, что аналогичное произойдет и в случае чисел вида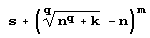 
при достаточно больших целых т и целых 5, k, n, q, удовлетворяющих неравенствам 1<k<n. Конечно, наверняка можно придумать и другие формулы, доставляющие "плохие" числа. Если все это исключения, то не слишком ли их много?! После всего сказанного, возможно, вы даже подозреваете, что неприятности будут вообще в случае чисел вида 1 +е при очень малых е, например при ε= 1/(1000!). Так вот она, непредсказуемость: при ε= 1/(10000!) все происходит без каких-либо неожиданностей. И вообще, при рациональных е неприятностей не бывает.
Недаром рациональный значит "разумный"! И уж если мы заговорили о разумном и рациональном, то не разумно ли было бы научиться рациональным способам проверки правильности полученных разложений в цепную дробь? Для этого нужно всего лишь научиться (с помощью системы Mathematica) находить числа по их представлению в виде цепных дробей. Оказывается, это совсем несложно, и именно к этому мы сейчас и перейдем.