Иллюстрированный самоучитель по Mathematica 5

Частные случаи разложения чисел в цепные дроби

Как видите, число оказалось на самом деле рациональным (числители выделены курсивом, а знаменатели – полужирным), а цепная дробь – конечной, но система Mathematica об этом не догадалась. Этот случай говорит о том, что иногда нужно подсказывать, что некоторые выражения можно упрощать. Без этого в данном случае разложение не получить.

Интерес представляют и полученные разложения: все их элементы равны 2, а количество элементов равно п. Никакие другие числа этим свойством не обладают.

Некоторые полезные разложения квадратичных иррациональностей в цепную дробь.

В задачниках часто используются разложения в цепную дробь квадратичных иррациональностей вроде:

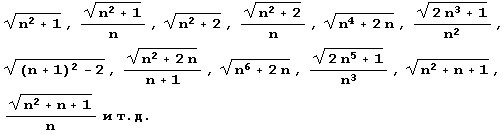
Составим таблицу разложения их в цепные дроби. Сначала определим нужные нам функции.

Вот как выглядит программа для разложения этих иррациональностей.

Результаты оформлены в виде таблицы.

Посмотрите внимательно на третий и четвертый столбцы этой таблицы. Вы увидите нечто весьма интересное: 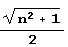при четном n разлагается в дробь {n/2,{4n,n}}, a при нечетном – в дробь ([n/2], {1.1,n}}. Что же касается более сложного выражения, 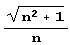, то несколько удивительно то, что его разложение даже проще: (1, {2n^2.2}}.

Составим таблицу разложения 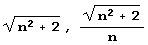и 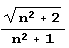в цепные дроби. Сначала определим нужные нам функции.

После выполнения программы составляем таблицу.

Из таблицы видно, что период всех дробей, являющихся разложением чисел 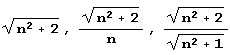состоит всего лишь из двух элементов. Несколько неожиданно то, что разложение самой простой из этих квадратичных иррациональностей, 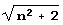, имеет, пожалуй, наиболее сложный период – все его элементы зависят от n. В периодах разложения двух "более сложных" иррациональностей, 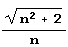, 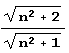лишь первый элемент периода зависит от n.

Правда, зависимость эта от n нелинейная, и это как бы "компенсирует" постоянство второго элемента периода.