Иллюстрированный самоучитель по Mathematica 5

Числа Фибоначчи и цепные дроби

Вот еще пример.

Сколько девяток во втором элементе? 13 = 8+5 = Fibonacci [7] – следующее число Фибоначчи. А сколько нулей? 21 = 13+8 = Fibonacci [8] – опять следующее число Фибоначчи! А сколько цифр во втором элементе? 21 + 13+1 = Fibonacci [9]+l – на единицу больше, чем следующее число Фибоначчи! Но эта единица не для того, чтобы портить картину, она как раз служит для того, чтобы утвердить закономерность, потому что благодаря ей второй элемент равен 10^F9 + 10^F7 -1.

Однако не при всех основаниях картина столь гармонична. Возьмем, например, в качестве основания:

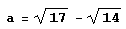
Числа вида:

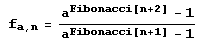
Могут доставить множество неприятностей при разложении в цепные дроби. Вот первая попытка получить первые десять элементов разложения в цепную дробь.

А вот и вторая:

Точность – два с половиной миллиона десятичных цифр! Куда ж еще увеличивать?!