Цепные дроби. Представление числа непрерывной дробью (функция Continued Fraction).
Функция ContinuedFraction [x] преобразует число д: в непрерывную дробь. Количество звеньев определяется точностью числа х. Следующая программа, например, находит представления первых 50 чисел Бернулли в виде цепных дробей.
Do[Print[2n, ":", ContinuedFraction[BernoulliB[2n]]], {n, 0.50}]Как видно из таблицы, некоторые числа Бернулли представляются цепной дробью с очень небольшим количеством звеньев.
Количество звеньев цепной дроби можно задать явно в качестве второго параметра.
Это позволяет получить наилучшие приближения числа дробями, знаменатели которых не превосходят некоторого числа. Пусть, например, нужно найти первые 20 звеньев цепной дроби, представляющей число:
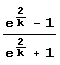
(Разложение этих чисел в цепную дробь при любом натуральном k было найдено Эйлером в 1737 году.) Вот нужная нам программа.
Do[Print[k, ":", ContinuedFraction[E ^ (2 / k), 20]], {k, 1.10}]Если у цепной дроби количество звеньев меньше заданного, будет сгенерировано предупреждение. Вот как выглядят, например, результаты разложения корней из 2 в цепную дробь с 20-ю звеньями.

Такое предупреждение, как видим, не препятствует работе программы.
