Разрядность и точность при выполнении операций над числами. Отбрасывание малых вещественных чисел (функция Chop).
Давайте теперь посмотрим, что происходит с разрядностью и точностью при выполнении действий.
Как и следовало ожидать, разрядность больше точности, поскольку число больше 1 и, следовательно, некоторые значащие цифры стоят до десятичной точки. Передвинем теперь точку на 3 разряда вправо, для чего умножим число на 1000, и посмотрим, изменится ли точность и разрядность.
Как видим, разрядность не изменилась, точность уменьшилась на 3, поскольку фактически теперь в дробной части на 3 цифры меньше. А что получится, если мы точку передвинем вправо? Для этого исходное число нужно разделить на 1000.
Разрядность, как и прежде, не изменилась, зато точность увеличилась на 3, поскольку добавилось три значащих разряда после точки.
А теперь давайте в исходном числе передвинем десятичную точку на 6 разрядов вправо. Для этого разделим его на 1 000 000. Тогда целая часть числа будет равна 0. Изменится ли при этом разрядность?
Разрядность при этом, как видите, не изменилась, но точность увеличилась и даже превзошла разрядность!
Отсюда можем заключить, что в то время как разрядность (количество значащих цифр) не зависит от положения десятичной точки, точность изменяется при изменении положения точки и может быть как меньше, так и больше разрядности. Кстати, а как система Mathematica определяет разрядность и точность? Почему эти числа не обязательно целые?
Чтобы узнать ответ на этот вопрос, давайте разберемся, как система Mathematica подсчитывает эти величины. Пусть задано приближенное значение вещественного числа х с погрешностью 6. Само число х можно рассматривать как десятичную дробь, для которой известны лишь некоторые разряды. Система Mathematica по заданному приближению числа х может считать, что число х лежит в интервале (х-b/2, х+b/2), длина которого равна погрешности 5. Тогда разрядность числа х определяется как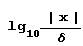 
а его точность – как 
.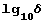