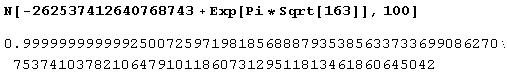Дробная часть вещественного числа (функция FractionalPart)
Пусть х – вещественное число. Тогда его дробную часть {х} можно определить равенством: {х} = х -[х]. По этому, общепринятому в математике определению дробная часть всегда неотрицательна и меньше единицы: 0<{х}<1. Однако в системе Mathematica используется несколько иное определение:
FractionalPart[x] = x - IntegerPart[x]Поэтому FractionalPart [х] отрицательна для нецелых отрицательных х.
Чтобы освоиться с функцией FractionalPart, напишем программу, которая распечатывает результат применения функции FractionalPart к каждому элементу списка. Прежде всего нам понадобится определить функцию, которая оформляет вывод следующим образом.
FractionalPart[ х ] – результат применения функции FractionalPart к х.
Вот как для этого можно определить функцию f.
f = (Print["FractionalPart[", #1,"]= ",FractionalPart[#1]] &)Теперь можем написать программу, в которой функция f применяется к каждому элементу списка.
f/@{x,2.4.0.3999999999999999',2.6.0.6000000000000001\-2.4,- 0.3999999999999999",-2.6,Pi,10,-Pi^2.2*Sin[1],Exp[Pi*Sqrt[163]]}Вот результат:
Давайте теперь вычислим:
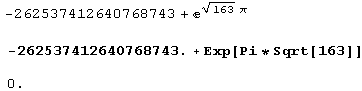
Неужели число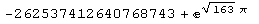 
равно нулю? Ведь это означает, что 
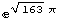целое. Давайте повторим вычисления.
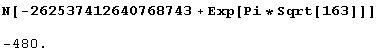
О, это уже какая-то загадка. Разные результаты при вычислении одного и того же выражения! А вот и разгадка: мы проводили вычисления с разной разрядностью, притом в обоих случаях точность была недостаточна. Давайте повторим вычисления с большей разрядностью.
