Дробная часть вещественного числа (функция FractionalPart)
Итак, все говорит о том, что эта гипотеза верна! А знаете, почему? Потому что ведущие нули не учитываются при подсчете значащих цифр (а ведь именно их количество и равно разрядности). "Ну, это я знал с шестого класса, если не с пеленок. Давайте лучше решим задачу до конца, раз уж мы столь тщательно проверили предложенный мною вариант программы и убедились в его правильности!" – воскликнет иной искушенный читатель. Что же, не возражаю. Давайте зададим параметры и получим результат.

Полужирным здесь выделены искомая сто первая тысяча цифр в представлении числа к десятичной дробью, причем первая выделенная цифра является стотысячной после запятой. "Ну вот, и все дела. Я сразу говорил, что нужно применить функцию FractionalPart. А автор все сомневался, проверял тривиальную программу, сравнивал десятичные знаки с предварительно вычисленными значениями я, измышлял гипотезы… Да в этой программе Pi можно заменить любым числом, в конце концов, я такие программы пишу с пеленок!" – возмутится тут искушенный читатель. Ой, не торопитесь делать такие выводы. В математике (и в программировании, и в компьютерной алгебре) есть великие идеи, но нет мелочей. А что касается вещественных чисел, то они свои ловушки расставляют не только на страницах учебников по теории функций вещественного переменного (чтобы изловить ленивых студентов), но и в вполне респектабельных программах (чтобы в эти ловушки на сей раз угодили "искушенные" читатели и нерадивые пользователи). Вспомните, что мы в ходе проверки подтвердили гипотезу о том, что количество ведущих нулей равно количеству "лишних" цифр. Но ведь мы заранее не знаем, сколько ведущих нулей может встретиться при вычислении дробной части FractionalPart [10^n*Pi], так что заранее ручаться за правильный выбор разрядности мы не могли! Нам просто повезло, что выбранное значение разрядности обеспечило нужную точность!
В принципе заранее неизвестно, работает ли наша программа для всех натуральных значений n и k. Указанного нами значения $MaxExtraPrecision = n+k+10 может ведь и не хватить для вычисления k+10 значащих цифр дробной части, если она будет начинаться более, чем с десяти нулей! Если бы в десятичном приближении я встречались сколь угодно длинные последовательности нулей, то для каждого k нашлось бы такое n, что программа с задачей не справилась бы! К счастью для "искушенного" читателя в настоящий момент это неизвестно. Зато даже шестиклассник (во всяком случае, участник районных математических олимпиад) без труда может придумать примеры вещественных чисел, для которых эта программа и ей подобные не работают. Нужно просто выбрать число, в десятичной записи которого встречаются все более длинные последовательности нулей. В качестве примера подойдет число 0.1234567891011121314151617181920…, в котором после десятичной точки выписаны последовательно все натуральные числа. Есть, конечно, и более экзотические примеры, что-нибудь вроде:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
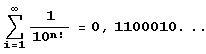
Десятичная запись этого числа содержит только нули и единицы, причем и тех, и других там бесконечно много, но единицы встречаются столь редко, что если наудачу выберешь какую-нибудь цифру, почти наверняка попадешь на последовательность нулей. Так что слухи о том, что придуманная нами программа при тривиальных модификациях может быть применена к любому вещественному числу, были несколько преувеличены…
