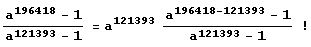Дробная часть вещественного числа (функция FractionalPart)
Упражнение 3.3.
Пусть:
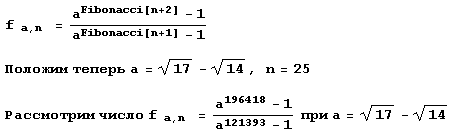
Сколько у этого числа нулей следует сразу после десятичной точки?
Решение.
Вот самое простое решение. Сначала вводим определение дроби fajl.
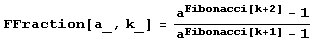
Теперь нужно вычислить число с такой точностью, чтобы найти хотя бы один ненулевой знак после запятой. Давайте попробуем.
N[FFraction[Sqrt[17] - Sqrt[14], 25], 50] 1.0000000000000000000000000000000000000000000000000Ну и как? А вот еще:
Хотите еще? Пожалуйста.
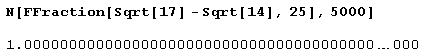
А пятьдесят тысяч знаков после десятичной точки не хотите ли? Хотите. Тогда пожалуйста, только эффект будет в десять раз сильнее.
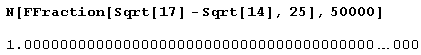
Между прочим, если это число целое, то после десятичной точки у него сплошные нули… И все попытки просто приведут к исчерпанию свободной памяти. Ну бывает же, что дроби сокращаются, а радикалы взаимно уничтожаются:
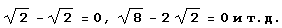
А здесь ведь разность степеней делится на разность степеней… Вот оно, коварство авторов, придумывающих "подленькие" задачи! Возможно, нужно лишь упростить выражение и убедиться, что оно равно какому-нибудь целому числу! Вот если в числителе вычесть и добавить удачно подобранную степень основания:
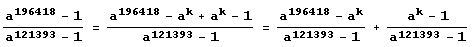
Конечно, сразу же просится k = 121393, тогда сразу же выделится единица:
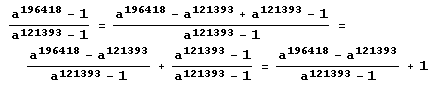
Осталось справиться с числом: